LV03-10-数据结构-树

发表于 分类于 ， ， 本文字数： 2.7k 阅读时长 ≈ 10 分钟

本文主要是数据结构——树的相关笔记，若笔记中有错误或者不合适的地方，欢迎批评指正😃。

点击查看使用工具及版本
Windows windows11
Ubuntu Ubuntu16.04的64位版本
VMware® Workstation 16 Pro 16.2.3 build-19376536
SecureCRT Version 8.7.2 (x64 build 2214) - 正式版-2020年5月14日
开发板 正点原子 i.MX6ULL Linux阿尔法开发板
uboot NXP官方提供的uboot，NXP提供的版本为uboot-imx-rel_imx_4.1.15_2.1.0_ga(使用的uboot版本为U-Boot 2016.03)
linux内核 linux-4.15(NXP官方提供)
STM32开发板 正点原子战舰V3(STM32F103ZET6)
点击查看本文参考资料
参考方向 参考原文
------
点击查看相关文件下载
--- ---

1.树的定义

树是一种非线性存储结构，存储的是具有一对多关系的数据元素的集合。树的一般形式如下图所示：

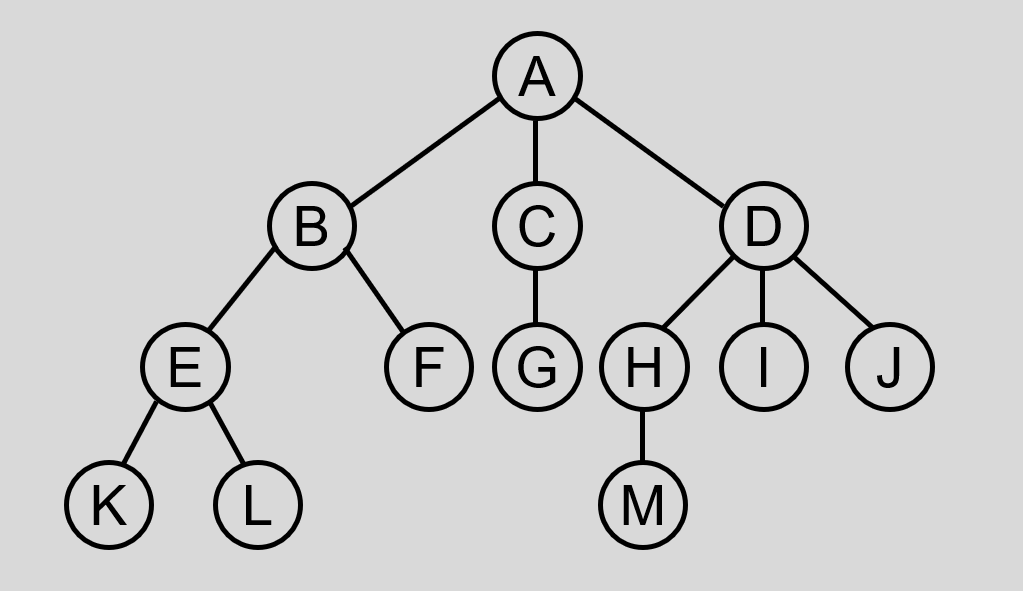
image-20220502073832348

任何一个非空树需要满足两个条件：

（1）有且仅有一个特定的称为根（ Root ）的节点；

（2）其余的节点可以分为 m （ m ≥ 0 ）个互不相交的有限集合 T1 、 T2 、……、 Tm ，其中每一个集合又是一棵树，并称为其根的子树。

2.树的表示

树的表示方法有一般表示法，文氏图表示法，凹入表示法和嵌套括号法。

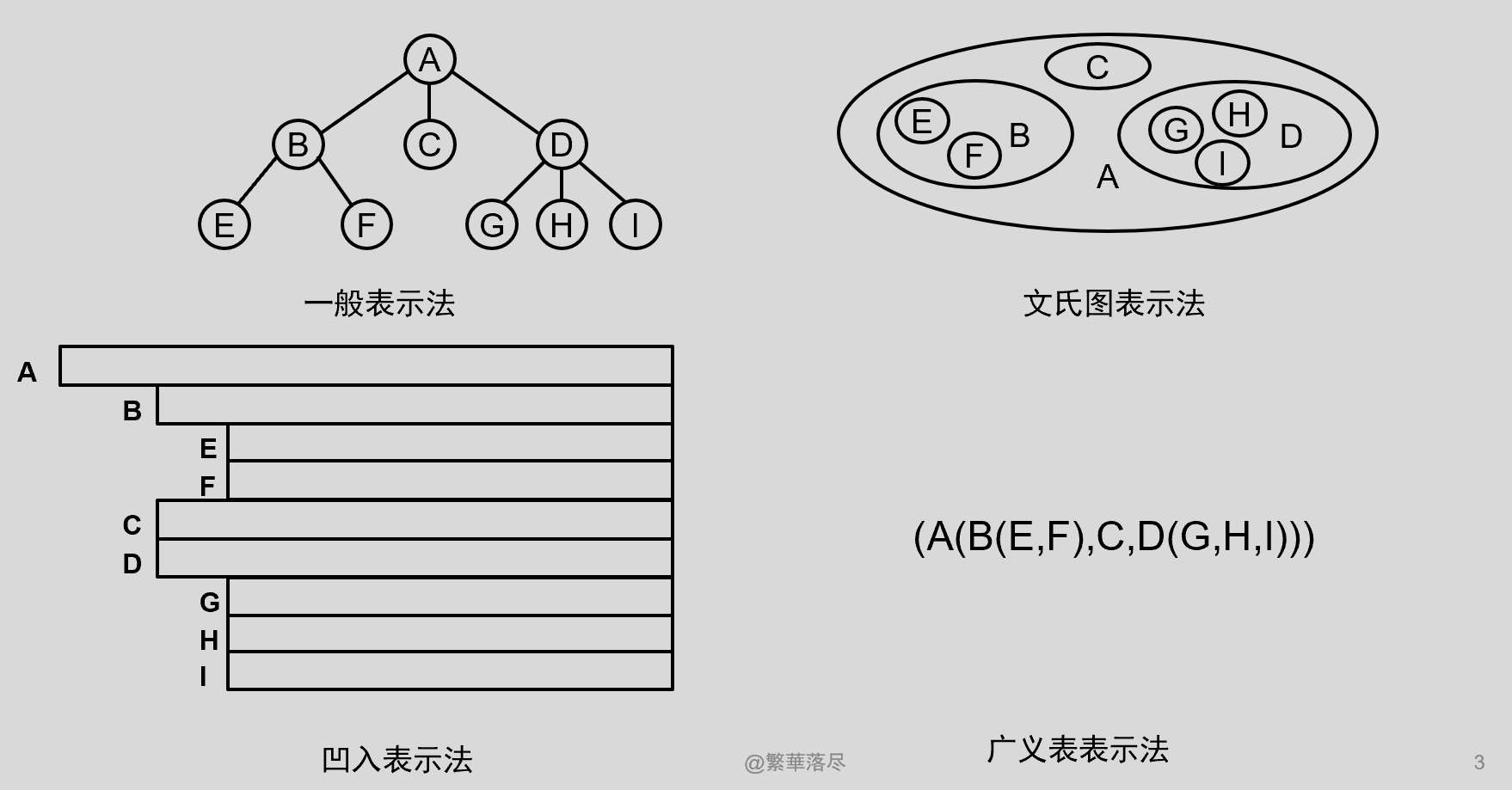
image-20220502080012595

3.基本概念

3.1结点

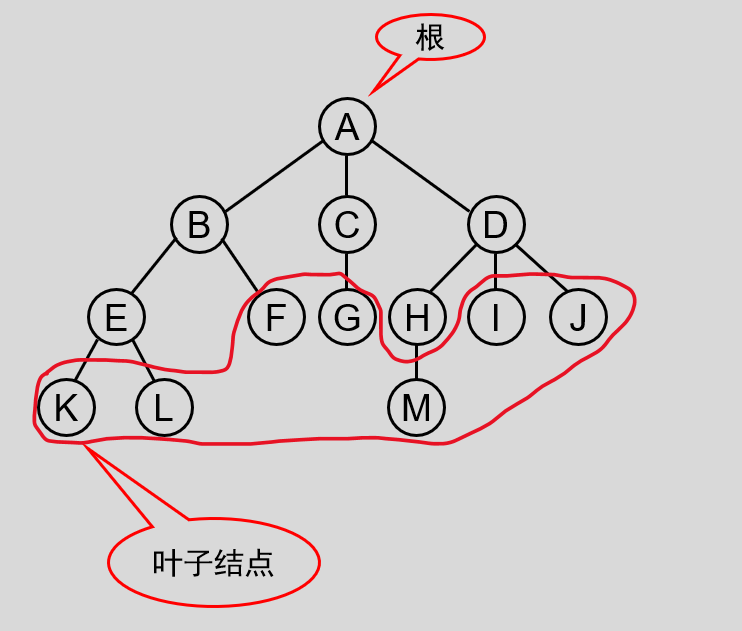
image-20220502083225413
  • 结点：使用树结构存储的每一个数据元素都被称为结点，如图中的 A ~ M 。
  • 父结点：上图中，对于结点 A 、 B 、 C 、 D 来说， A 就叫做 B 、 C 、 D 的父结点，也叫双亲节点。
  • 子结点：上图中，对于结点 A 、 B 、 C 、 D 来说， B 、 C 、 D 就叫做 A 的子结点，也叫孩子结点。
  • 兄弟节点：上图中，对于结点 A 、 B 、 C 、 D 来说， B 、 C 、 D 具有相同的父结点，所以它们互为兄弟结点。
  • 根节点：每一个非空树都有且只有一个被称为根的结点，如上图中的 A 。判别依据：若一个结点没有父结点，那么这个结点就是整棵树的根结点。
  • 叶子结点：上图中，对于结点 K 、 L 、 F 、 G 、 M 、 I 、 J ，它们 没有任何子结点，那么这些结点就叫做叶子结点，也叫终端结点（叶子结点的度为 0 ）。
  • 分支结点：度数不为零的节点称为分支节点。
  • 内部结点：除根节点外的分支节点称为内部节点。

3.2空树与子树

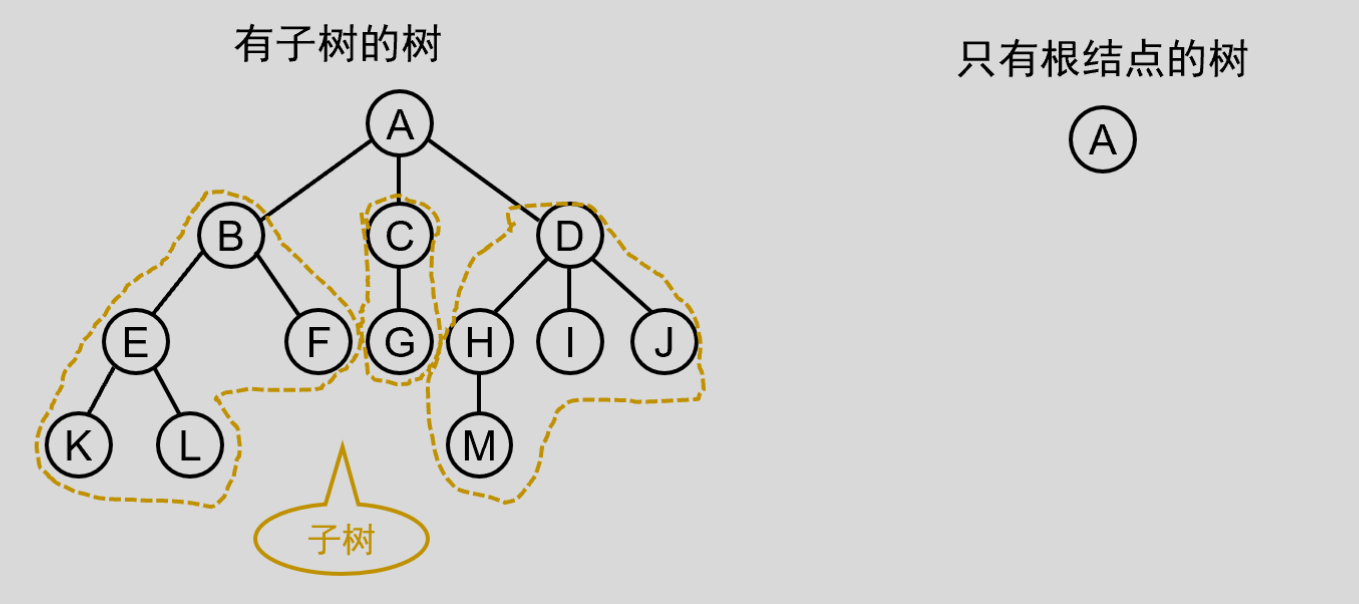
image-20220502083528569
  • 空树：若集合为空，那么它将可以构成一个没有结点的空树。
  • 子树：上图中，整棵树的根节点为 A ，只看 B 、 E 、 F 、 K 、 L ，那么这也是一个树的结构，并且结点 B 为根结点，所以 B 、 E 、 F 、 K 、 L 组成的树称为整个树的子树。同样， E 、 K 、 L 也构成一颗子树，根结点为 E ； C 、 G 也构成子树，根节点为 C 。

【注意】

（1）单个结点也是一棵树，且根节点为结点本身。

（2）在树的结构中，对于同一个结点的各个子树之间不可以有交集，若有，那将不符合树的结构了。

3.3度和层次

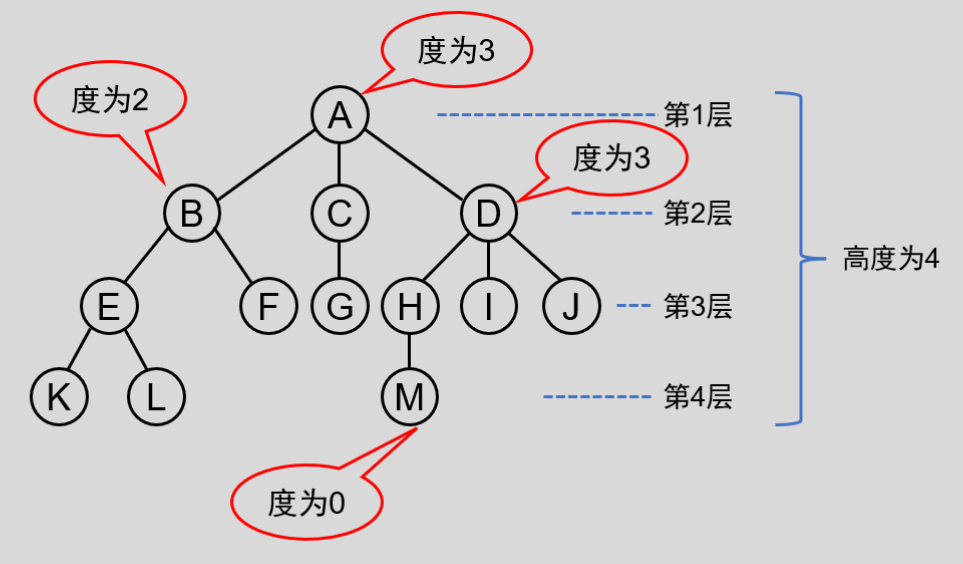
image-20220502083759939

  • 结点的度：对于树的一个结点所拥有子树的个数称之为结点的度( Degree )，度也可以说是一个结点下有多少个分支。例如上图中的结点 A ，它下边有三个子树（三个分支），所以结点 A 的度为 3 ；对于结点 M ，度为 0 。

  • 树的度：一棵树的度数是指这个树中结点的最大度数，上图中，各个结点度的最大值为 3 ，所以这颗树的度数为 3 。

  • 结点层次：从树根开始，树根所在层为第 1 层，根的孩子结点所在的层为第 2 层，如图中所示。 A 结点在第 1 层， B 、 C 、 D 为第 2 层， E 、 F 、 G 、 H 、 I 、 J 在第 3 层， K 、 L 、 M 在第 4 层。

  • 堂兄弟：双亲在同一层的结点互为堂兄，图中结点 G 与 E 、 F 、 H 、 I 、 J 互为堂兄弟。

  • 树的深度：一棵树的深度（高度）是树中结点所在的最大的层次，上图中树的高度为 4 。

【注意】

（1）结点的层次等于这个结点的父结点层数加 1 。

（2）根节点层数定义为 1 。

3.4路径与祖先

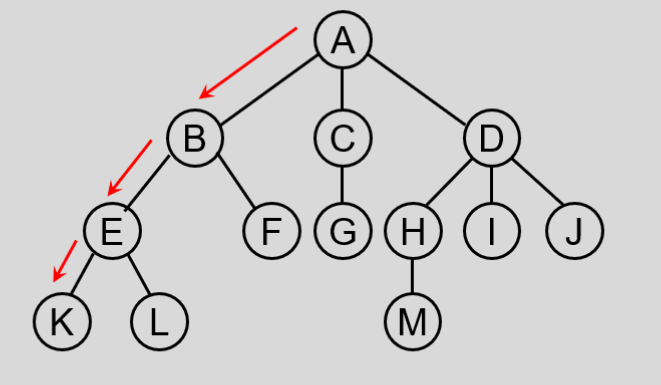
image-20220502085149575
  • 路径：一个结点系列$k_1, k_2, …… , k_i,k_{i+1}, ……, k_j$并满足$k_i$是$k_{i+1}$的父节点，就称为一条从$k_1$到$k_j$的路径。路径的长度为 j-1 ,即路径中的边数。
  • 祖先与子孙：路径中前面的节点是后面节点的祖先，后面节点是前面节点的子孙。

3.5有序树和无序树

若树中每个节点的各个子树的排列为从左到右，不能交换，即兄弟之间是有序的，则该树称为有序树。反之称为无序树。

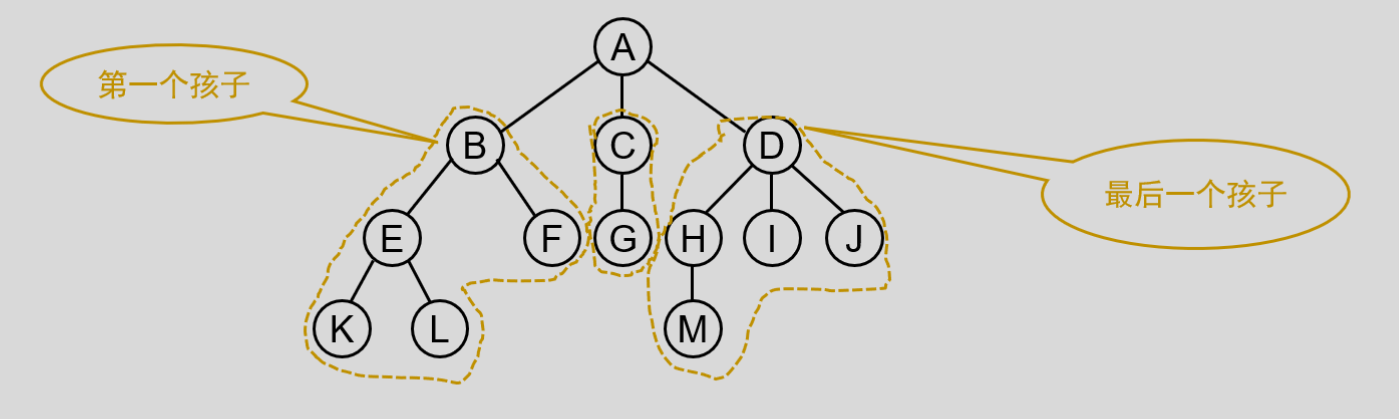
image-20220502085927073

如上图，如果是其本身是一棵有序树，则以结点 B 为根结点的子树为整棵树的第一个孩子，以结点 D 为根结点的子树为整棵树的最后一个孩子。

3.6森林

由 m （ m >= 0 ）个互不相交的树组成的集合被称为森林。树可以理解为是由根结点和若干子树构成的，而这若干子树本身是一个森林，所以，树还可以理解为是由根结点和森林组成的。用一个式子表示为：

1
2
3
4
Tree =（root,F）
    
root 表示树的根结点，
F 表示由 m（m >= 0）棵树组成的森林。

【注意】树去掉根节点就成为森林，森林加上一个新的根节点就成为树。

3.7树的逻辑结构

树中任何节点都可以有零个或多个直接后继节点（子节点），但至多只有一个直接前趋节点（父节点）。

根节点没有前趋节点，叶节点没有后继节点。

4.基本性质

（1）树的结点数等于所有结点度数加 1 。

【证明】每个结点的度数分别对应这个结点的子结点，假设所有结点的度数为b，那么结点数n = b + root = b +1。

（2）度为 m 的树中，第 i 层上至多有$m^{i-1}$个结点（ i ≥ 1 ）。

【证明】由数学归纳法证明

1.当树为第1层时，第1层至多有$m^0=1$个结点;
2.当树为第 i-1 层时，由该性质得第 i - 1层至多有$m^{i-2}$个结点;
3.当树为第 i 层时，由于树的度为 m ，可知每个第 i - 1 层的每个结点至多有 m 个子结点，因此第 i 层至多有$m^{i-2}*m=m^{i-1}$个结点。
由数学归纳法可知，上述结论正确。

（3）高度为 h 的 m 叉树至多有$(m^{h-1})/(m-1)$个结点。

【证明】

由性质(1)可知，度为 m 的树第 i 层至多有$m{i-1}$个结点；

因此高度为 h 的 m 叉树至多有 $n = m^0+m^1+…+m^{h-1}$个结点；

用等比数列求和公式，公比为 m ，可以得到结点数$n= (m^h-1)/(m-1)$。

（3）具有 n 个结点的 m 叉树的最小高度为$[\log_m[n*(m-1)+1]]$

【证明】

由性质(2)逆推，要得到 m 叉树的最小高度，那么每一层都具有最多的结点，由于高度为整数，且多余结点也是一层，所以树的高度需要向上取整。