LV03-09-数据结构-队列

发表于 分类于 ， ， 本文字数： 5.7k 阅读时长 ≈ 21 分钟

本文主要是数据结构——队列相关笔记，若笔记中有错误或者不合适的地方，欢迎批评指正😃。

点击查看使用工具及版本
Windows windows11
Ubuntu Ubuntu16.04的64位版本
VMware® Workstation 16 Pro 16.2.3 build-19376536
SecureCRT Version 8.7.2 (x64 build 2214) - 正式版-2020年5月14日
开发板 正点原子 i.MX6ULL Linux阿尔法开发板
uboot NXP官方提供的uboot，NXP提供的版本为uboot-imx-rel_imx_4.1.15_2.1.0_ga(使用的uboot版本为U-Boot 2016.03)
linux内核 linux-4.15(NXP官方提供)
STM32开发板 正点原子战舰V3(STM32F103ZET6)
点击查看本文参考资料
参考方向 参考原文
------
点击查看相关文件下载
--- ---

一、队列的概念

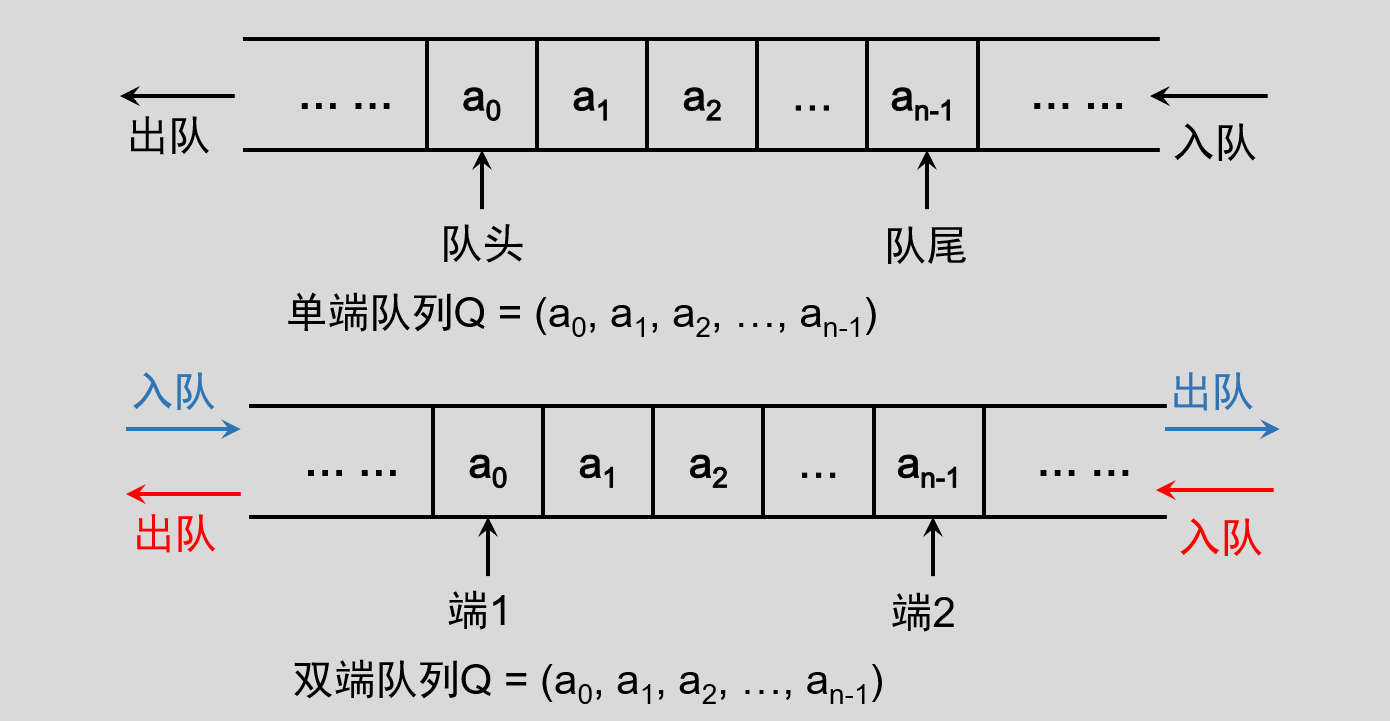
队列是限制在两端进行插入操作和删除操作的线性表。

  • 队尾：允许进行存入操作的一端称为队尾。
  • 队头：允许进行删除操作的一端称为队头。
  • 空队：当线性表中没有元素时，称为空队。
  • 入队：数据元素进队列的过程称为入队。
  • 出队：数据元素出队列的过程称为 出队。

队列的特点是先进先出（ FIFO ），数据从队列的一端进，从另一端出，可以由顺序表实现队列的存储结构，称为顺序队列，也可以由链表实现队列的存储结构，称为链式队列。两者的区别仅是顺序表和链表的区别，即在实际的物理空间中，数据集中存储的队列是顺序队列，分散存储的队列是链队列。

队列可以是单端的，也可以是双端的，但是定要遵循的是先进先出的规则，从一端进，从另一端出。

image-20220501085957416

二、顺序队列

1.存储结构

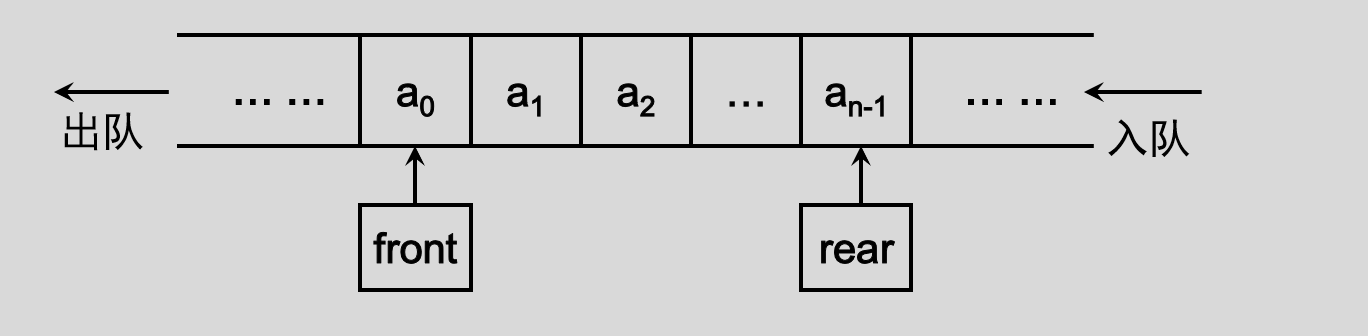
顺序队列是一种顺序存储结构，它借助顺序表实现，由于我们需要在顺序表的一端实现入队，在另一端实现出队，所以需要两个”指针”（为什么加引号呢？严格来说这两个并非是指针变量，而只是代表了顺序队列中指向队头元素和队尾元素所在数组位置下标的变量，一般是整型数据），来指向队头和队尾。

image-20220501091028672

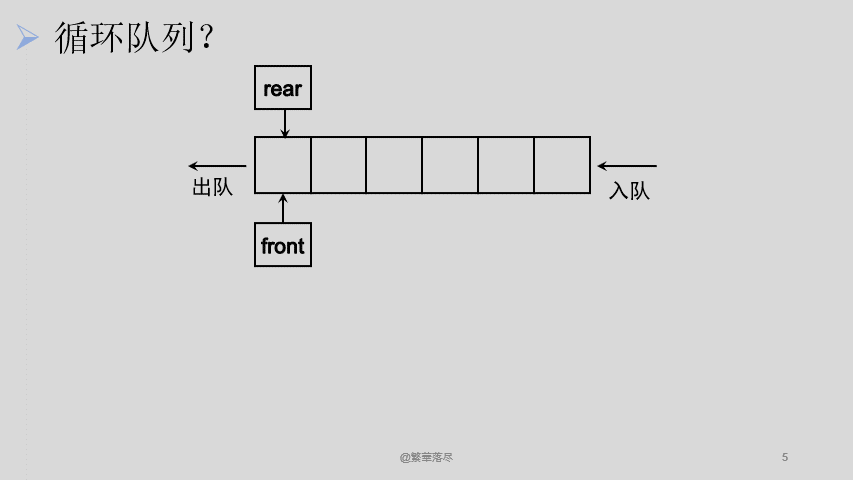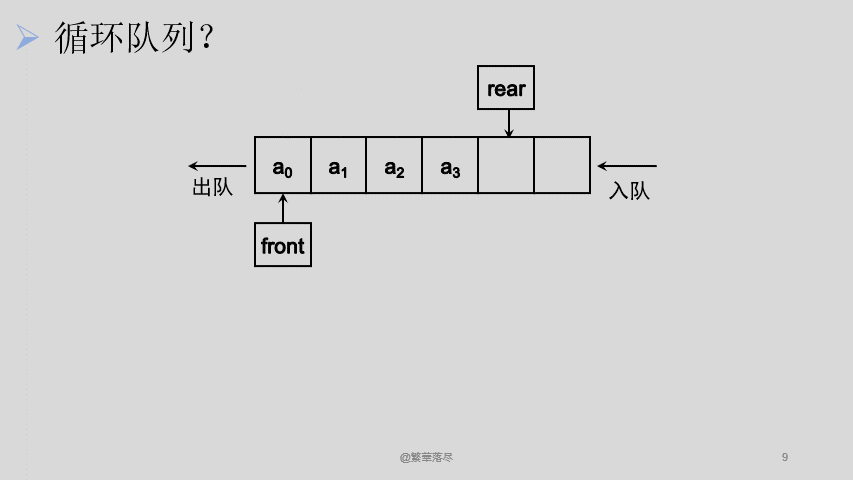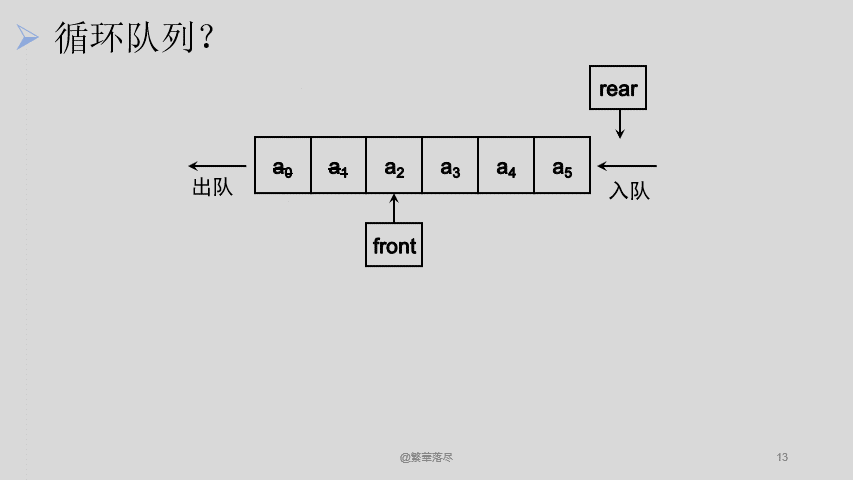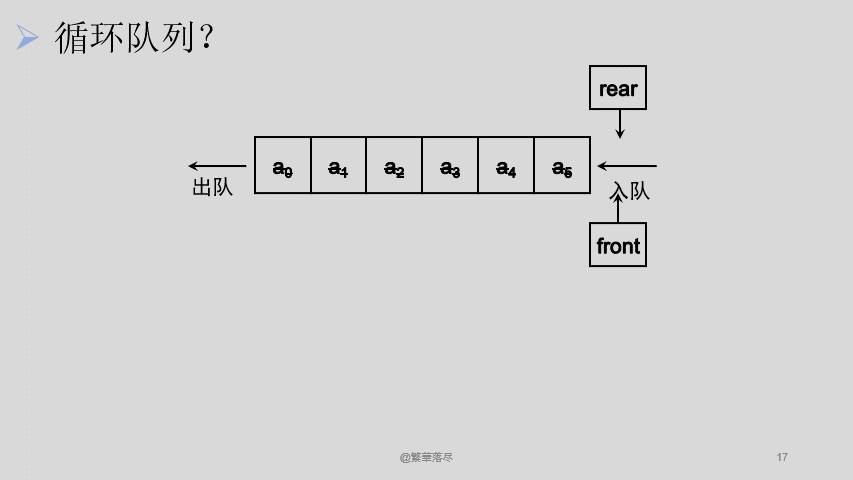
按照预想的情况应该是上图的这种结构， front 指向队头元素， rear 指向队尾元素的下一个位置（原因？只有指向下一个位置才能插入嘛，不然这个数据不就被覆盖了嘛，哈哈），接下来我们想象一下从数据入队到全部出队，会发生什么现象。假设有一个队列最大可以有 5 个元素，那么我们让 5 个数据入队然后再出队，然后来看一下最终的状态。

1

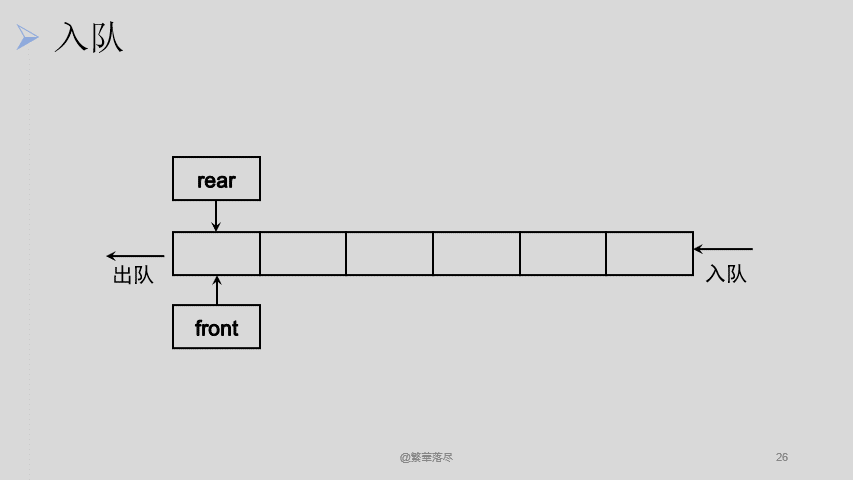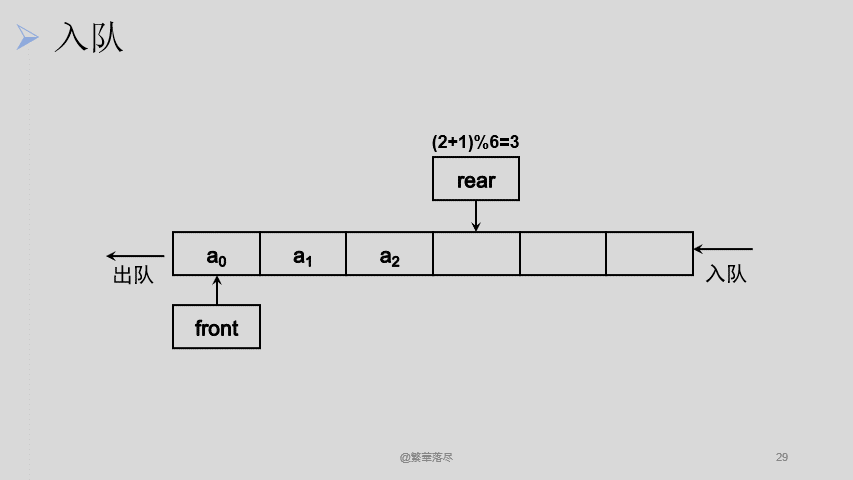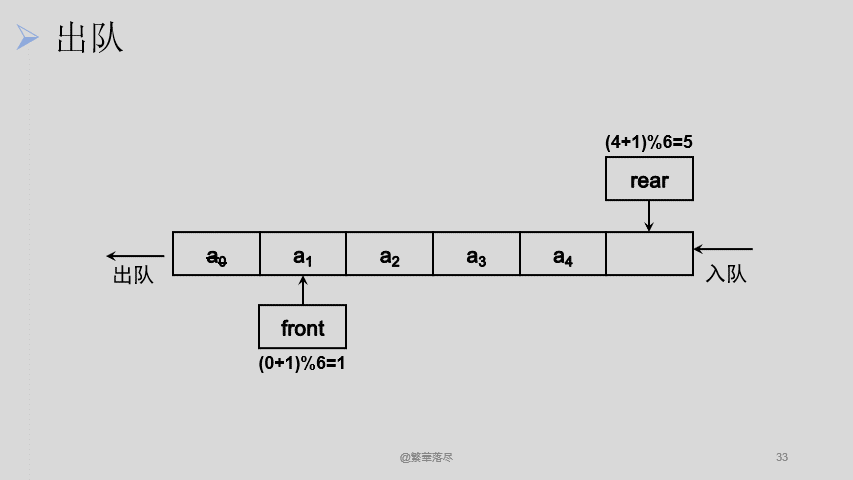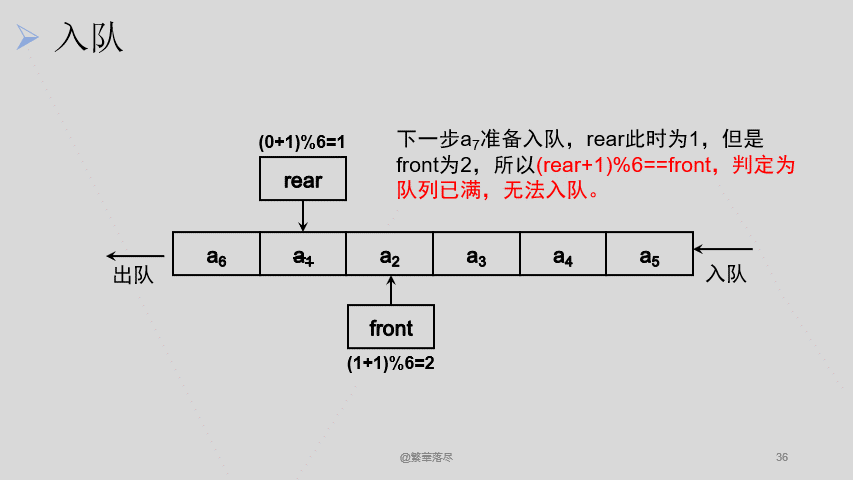
我们会发现入队的时候尾指针不断向后移动，出队的时候头指针也是不断向后移动，当头尾指针重合时，队列中没有元素，为空队。那么问题产生了，这个时候这个队列是空的，但是队头和队尾已经移动到最后边去了，前边即便空间已经空出来了，由于队列的规则限制，这意味着前边的内存空间是无法使用了，重新申请一个内存空间嘛？显然不太可能喽。那有什么办法吗？可以这样想，我们让队头和队尾指针再重头开始不就行了吗？方案是可行的，那怎么实现呢？

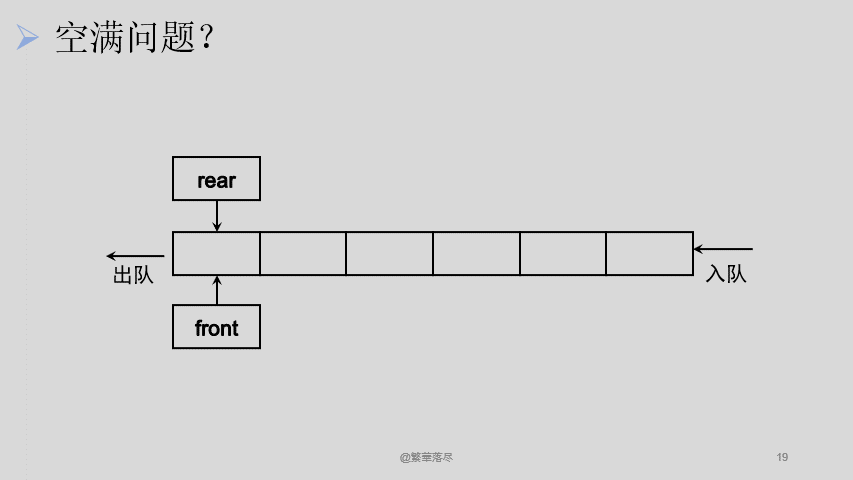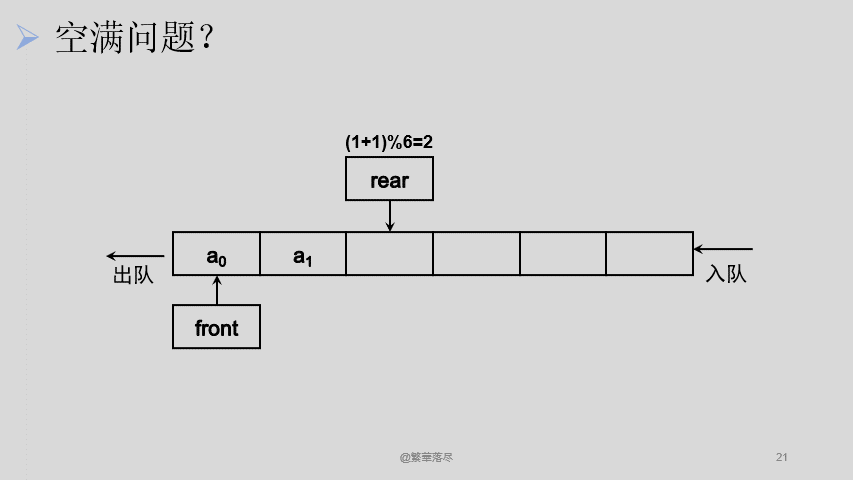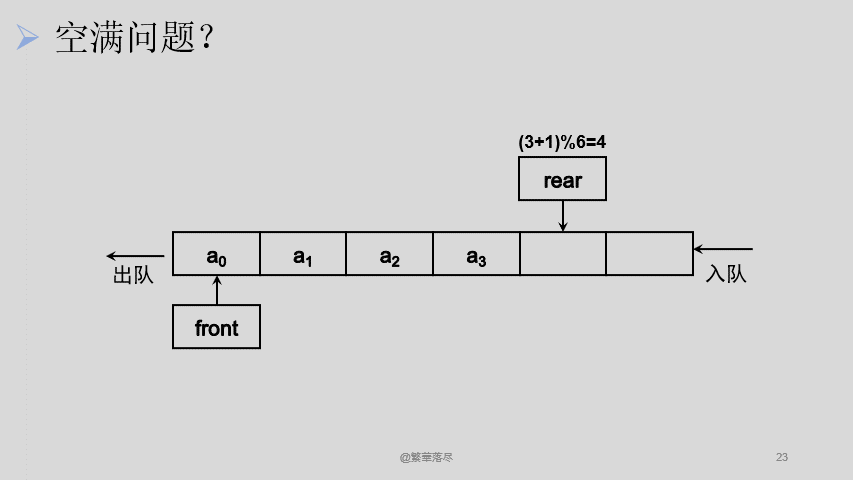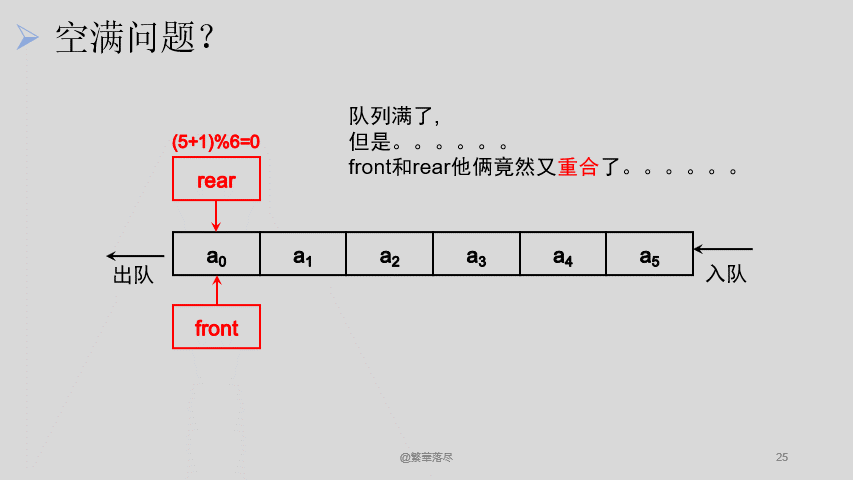
现在要解决的问题就是如何让 front 和 rear 一直自加还能保证只在这 6 个元素的队列中循环，也就是说，不管这两个指针加了多少次，是最后的取值只能在 0-5 之间，这个时候可以想到，不是有个取余数的操作嘛，对 6 取余的话，最后得到的余数一定是小于 6 的，这样，这个问题就解决啦。那我们看看还会不会有问题。

2

绝了，循环倒是实现了，但是，队满的时候，头尾指针重合了，这不完了。这样的话，我不知道它是空是满，万一这个状态是满的，我又继续入队了，那数据不就没得了？这又怎么办呢？没办法，只好牺牲掉数组的一个数据啦，这样当 rear 到最后一个位置的时候就不能再入队了，因为再入一个数据就已经满队了，再经过规则限定，我们来看看最后的效果吧。

3

【总结】

（1） front 指向队头元素的位置; rear 指向队尾元素的下一个位置。

（2）在队列操作过程中，为了提高效率，以调整指针代替队列元素的移动，并将数组作为循环队列的操作空间。

（3）为区别空队和满队，满队元素个数比数组元素个数少一个。

2.结构体实现

1
2
3
4
5
6
7
8
9
10
11
12
/* 宏定义 */
#define N 6   /* 定义队列的容量 */

/* 自定义数据类型 */
typedef int data_t; /* 定义栈中数据元素的数据类型 */

typedef struct 
{
	data_t data[N];  /* 用数组作为队列的储存空间 */
	int front;       /* 指示队头位置的指针 */
	int rear;        /* 指示队尾位置的指针 */
}seqqueue;           /* 顺序队列类型定义 */

【说明】顺序队列应为为 sequence queue ，所以后续使用 seqqueue 作为顺序队列结构体以及函数命名的关键字。

3.顺序队列基本操作

相关源代码可以在这里下载：

数据结构 队列 (密码:6sez)

3.1创建

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @Function: seqqueue_create
 * @Description: 顺序队列创建
 * @param   : none
 * @return  : 返回一个地址
 *            NULL,创建失败;
 *            other,创建成功
 */
seqqueue * seqqueue_create() 
{
	/* 创建一个顺序队列结构体指针变量 */
    seqqueue *sq;
	/* 1. 申请内存空间 */
	sq = (seqqueue *)malloc(sizeof(seqqueue));
	/* 2. 判断是否申请成功 */
	if(sq == NULL)
	{
		printf("sequence queue malloc failed!\n");
		return NULL;
	}
	/* 3. 初始化申请的内存空间 */
	memset(sq->data, 0, sizeof(sq->data));
	sq->front = 0;
	sq->rear = 0;
	
	return sq;
}

3.2释放

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @Function: seqqueue_free
 * @Description: 顺序队列释放
 * @param sq: 顺序队列地址
 * @return  : 返回一个NULL
 *            NULL,释放完毕
 */
seqqueue * seqqueue_free(seqqueue *sq) 
{
	/* 1. 判断顺序队列是否存在 */
	if(sq == NULL)
	{
		printf("sequence queue is not existed!\n");
		return NULL;
	}
	/* 2. 释放结构体指针变量指向的空间 */
	free(sq);
	sq = NULL;
	printf("sequence queue free completed!\n");
	return NULL;
}

3.3显示

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * @Function: seqqueue_show
 * @Description: 顺序队列显示
 * @param sq: 顺序队列地址
 * @return  : 返回一个数值
 *            0,显示完毕;
 *            -1,顺序队列不存在或者队列为空
 */
int seqqueue_show(seqqueue *sq) 
{
	int i = 0;
	/* 1. 判断顺序队列是否存在 */
	if(sq == NULL)
	{
		printf("sequence queue is not existed!\n");
		return -1;
	}
	/* 2. 判断顺序队列是否为空 */
	if(sq->front == sq->rear)
	{
		printf("sequence queue is empty!\n");
		return -1;
	}
	/* 3. 访问顺序队列中所有数据 */
	if(sq->front < sq->rear)
	{
		printf("sequence queue:");
		for(i = sq->front; i < sq->rear; i++)
		{
			printf("%d ", sq->data[i]);
		}
		puts("");
	}
	else
	{
		printf("sequence queue:");
		for(i = 0; i < N; i++)
		{
			if(i == sq->rear)
				printf("null ");
			else
				printf("%d ", sq->data[i]);
		}
		puts("");
	}
	
	return 0;
}

3.4入队

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @Function: seqqueue_enqueue
 * @Description: 入队
 * @param sq: 顺序队列地址
 * @param value: 入队数据
 * @return  : 返回一个数值
 *            0,入队成功;
 *            -1,入队失败
 */
int seqqueue_enqueue(seqqueue *sq, data_t value) 
{
	/* 1. 判断顺序队列是否存在 */
	if(sq == NULL)
	{
		printf("sequence queue is not existed!\n");
		return -1;
	}
	/* 2. 判断顺序队列是否已满 */
	if((sq->rear + 1) % N == sq->front)
	{
		printf("sequence queue is full!\n");
		return -1;
	}
	/* 3. 元素入队 */
	sq->data[sq->rear] = value;
	sq->rear = (sq->rear + 1) % N;
	
	return 0;
}

3.5出队

【注意】这里出队的时候不要做队列是否存在以及是否为空的判断，这两个判断若是有返回值的话程序会认为返回值就是出队的元素，所以队列的存在性以及是否为空，要在使用出队函数前进行判断。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
**
 * @Function: seqqueue_dequeue
 * @Description: 出队
 * @param sq: 顺序队列地址
 * @return  : 返回一个数据
 *            ret,出队数据
 */
data_t seqqueue_dequeue(seqqueue *sq) 
{
	/* 定义一个暂存队列元素的变量 */
	data_t ret;
	/* 1. 判断顺序队列是否存在 */
	/* 需要在函数外进行，这是因为该函数需要返回队列数据，队列数据也可能为这里的返回值 */
	/* 2. 判断顺序队列是否为空 */
	/* 需要在函数外进行，这是因为该函数需要返回队列数据，队列数据也可能为这里的返回值 */
	/* 3. 元素出队*/
	ret = sq->data[sq->front];
	/* 4. 更新队头指针 */
	sq->front = (sq->front + 1) % N;
	
	return ret;
}

3.6空满

点击查看判断是否为空函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @Function: seqqueue_empty
 * @Description: 顺序队列是否为空
 * @param sq: 顺序队列地址
 * @return  : 返回一个数值
 *            0,顺序队列非空;
 *            1,顺序队列为空;
 *            -1,顺序队列不存在
 */
int seqqueue_empty(seqqueue *sq) 
{
	/* 1. 判断顺序队列是否存在 */
	if(sq == NULL)
	{
		printf("sequence queue is not existed!\n");
		return -1;
	}
	/* 2. 判断队头队尾指针是否重合 */
	if(sq->front == sq->rear)
		return 1;
	else
		return 0;
	/* 或者可以写成下边的形式 */
	// return (sq->front == sq->rear ? 1 : 0);
}
点击查看判断是否为满函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * @Function: seqqueue_full
 * @Description: 顺序队列是否已满
 * @param sq: 顺序队列地址
 * @return  : 返回一个数值
 *            0,顺序队列未满;
 *            1,顺序队列已满;
 *            -1,顺序队列不存在
 */
int seqqueue_full(seqqueue *sq) 
{
	/* 1. 判断顺序队列是否存在 */
	if(sq == NULL)
	{
		printf("sequence queue is not existed!\n");
		return -1;
	}
	/* 2. 判断是否已满 */
	if((sq->rear + 1) % N == sq->front)
		return 1;
	else
		return 0;
}

3.7清空

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * @Function: seqqueue_clear
 * @Description: 顺序队列清空
 * @param sq: 顺序队列地址
 * @return  : 返回一个数值
 *            0,顺序队列已清空;
 *            -1,顺序队列不存在
 */
int seqqueue_clear(seqqueue *sq) 
{
	/* 1. 判断顺序队列是否存在 */
	if(sq == NULL)
	{
		printf("sequence queue is not existed!\n");
		return -1;
	}
	/* 2. 清空顺序队列 */
	sq->rear = sq->front = 0;

	return 0;
}

三、链式队列

1.存储结构

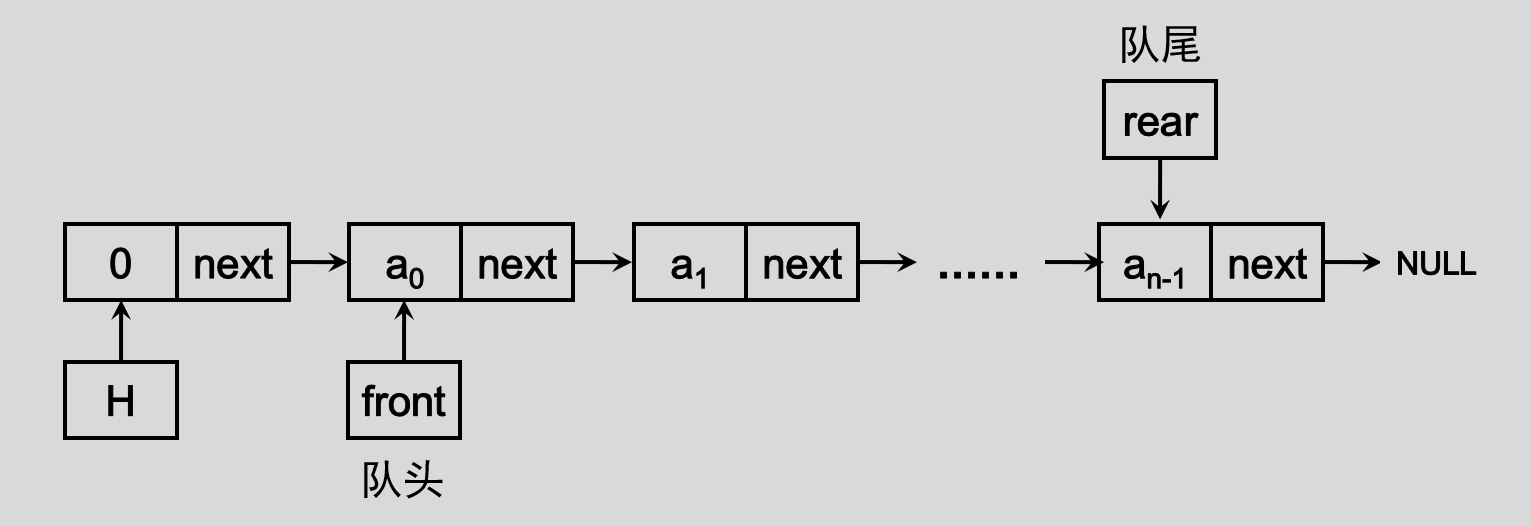
链式队列的存储结构如下图所示，将从队尾入队，队头出队：

image-20220501161801389

相对于顺序队列，链式队列没有假溢出，因为它不会满，链式队列入队操作会申请内存新建节点，出队会释放相应节点，动态存储，只要能成功申请内存创建新的节点，链式队列就不会满，所以不涉及溢出和队满的情况。（当然了，内存不够的时候也还是会满的啦，不过这个时候就可能需要考虑换更大空间的内存啦，哈哈哈。）

2.结构体实现

对于链式队列，还是借助单链表来实现，然后我们再添加头尾指针指向头尾就好啦。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 自定义数据类型 */
typedef int data_t; /* 定义栈中数据元素的数据类型 */

typedef struct slqueue_node 
{
	data_t data;
	struct slqueue_node *next;
}slqueuenode, * slqueuelink;

typedef struct 
{
	slqueuelink front;
	slqueuelink rear;
}slqueue_sq;

【说明】单链表实现的队列，英文名字是 single linked list queue ，所以我后边都用 slqueue 作为链式队列结构体及函数命名的关键词啦。

3.链式队列基本操作

相关源代码可以在这里下载：

数据结构 队列 (密码:6sez)

3.1创建

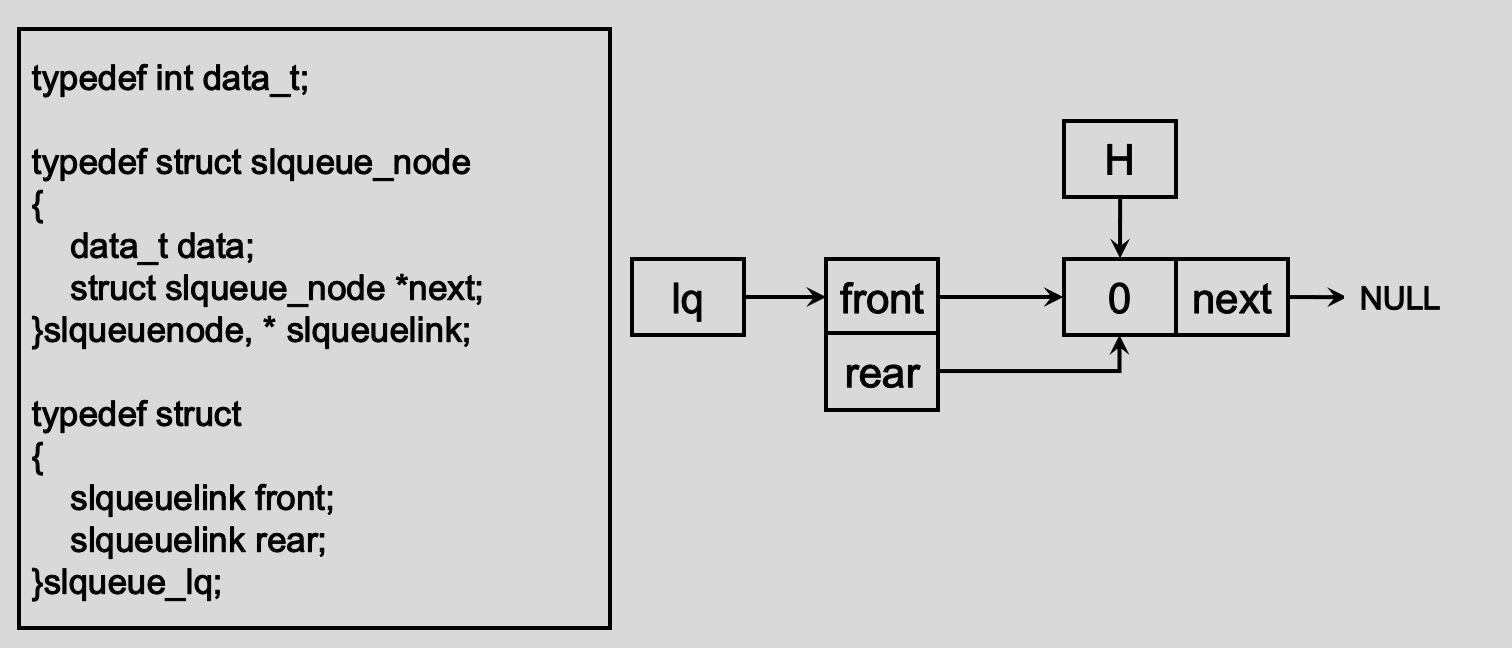
  • （1）链式队列结构体变量 lq 申请内存(包含两个成员： front 和 rear )；
  • （2）申请一个单链表结构体变量 Head 申请内存空间，也就是头节点的内存空间；
  • （3）队列结构体指针变量成员的首尾指针均指向 Head ；
  • （4）初始化单链表结构体变量成员
image-20220501175330538

【注意】（2）、（3）两步可合并，省去 Head 变量的定义即有：

1
lq->front = lq->rear = (slqueuelink)malloc(sizeof(slqueuenode));
点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * @Function: slqueue_create
 * @Description: 链式队列创建
 * @param   : none
 * @return  : 返回一个地址
 *            NULL,创建失败;
 *            other,创建成功
 */
slqueue_lq * slqueue_create() 
{
	/* 定义一个链式队列的结构体指针变量 */
	slqueue_lq *lq;
	/* 1. 申请链式队列结构体变量的内存空间(头尾指针内存空间) */
	lq = (slqueue_lq *)malloc(sizeof(slqueue_lq));
	/* 2. 判断链式队列结构体指针变量内存是否申请成功 */
	if(lq == NULL)
	{
		printf("single linked list queue malloc failed!\n");
		return NULL;
	}
	/* 3. 申请一个节点的内存空间(相当于申请一个链表头节点) */
	lq->front = lq->rear = (slqueuelink)malloc(sizeof(slqueuenode));
	/* 4. 判断节点是否申请成功 */
	if(lq->front == NULL)/* front和rear开始都指向头节点,用谁都可以 */
	{
		printf("single linked list queue node malloc failed!\n");
		free(lq);/* 释放掉之前申请的链式队列结构体指针变量内存空间 */
		return NULL;
	}
	/* 5. 初始化头节点 */
	lq->front->data = 0;
	lq->front->next = NULL;
	
	return lq;
}

3.2入队

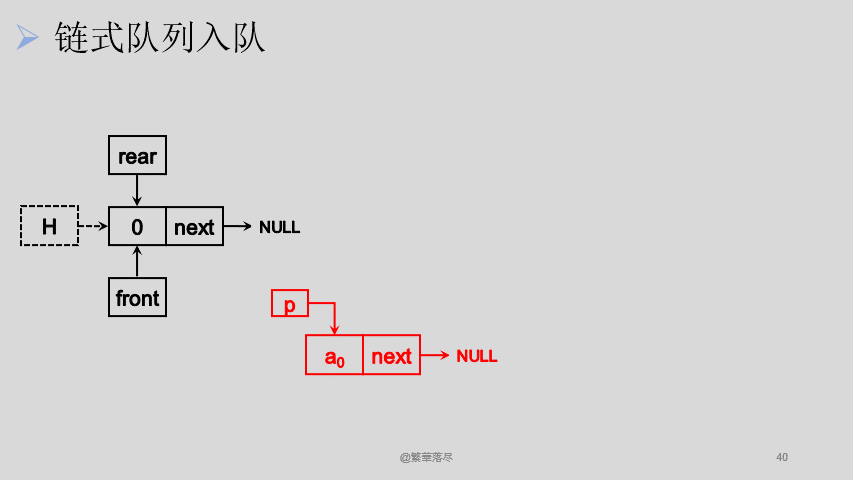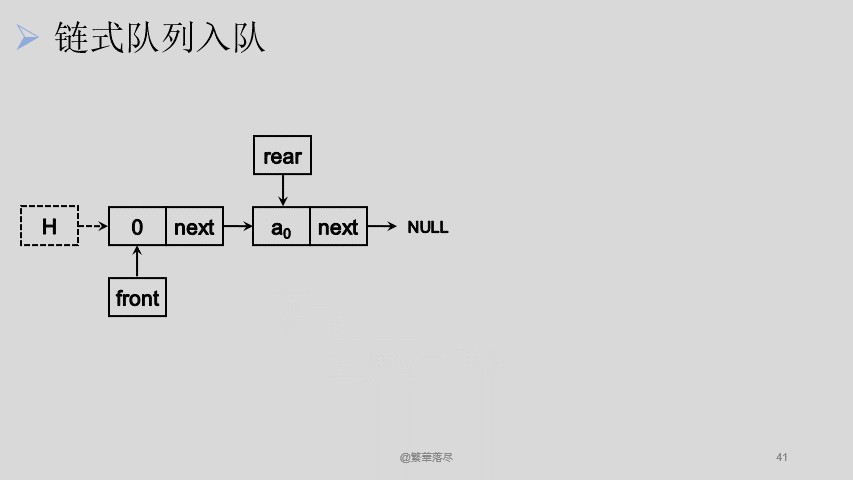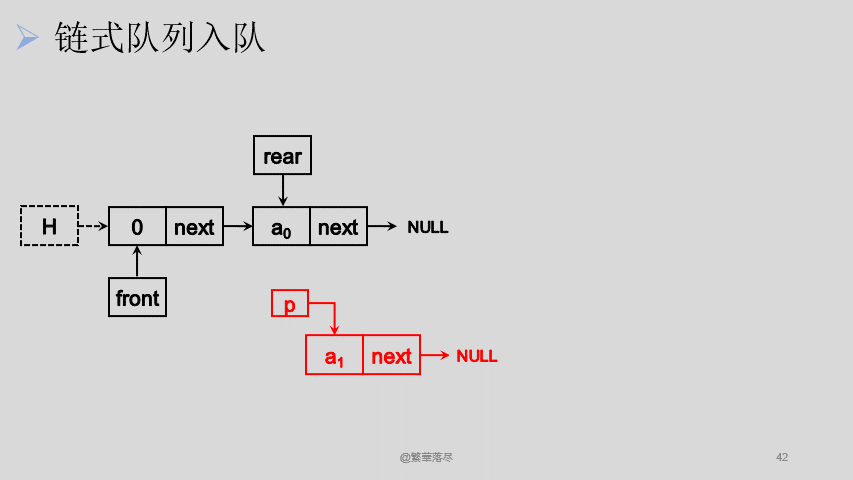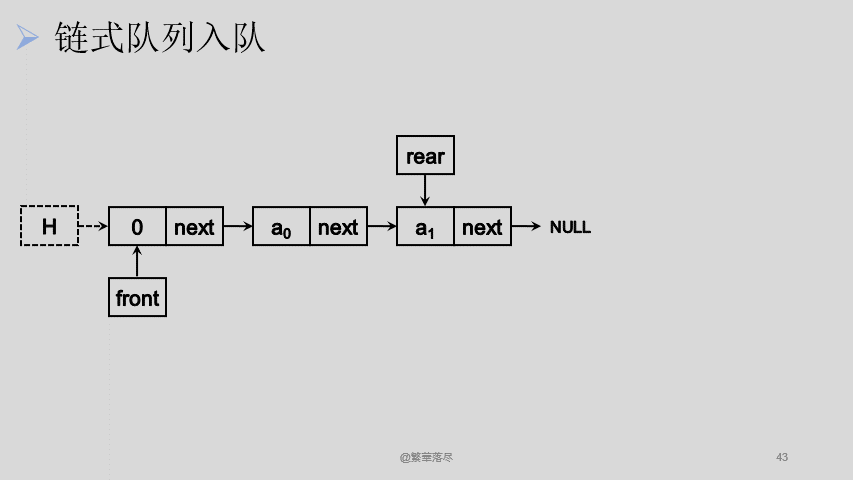
我们从链表尾进行入队操作：

4
点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * @Function: slqueue_enqueue
 * @Description: 链式队列入队
 * @param lq: 链式队列地址
 * @param value: 要入队的数据
 * @return  : 返回一个数值
 *            0,入队成功;
 *            -1,链式队列不存在或者新建节点失败
 */
int slqueue_enqueue(slqueue_lq *lq, data_t value) 
{
	/* 定义一个链式队列节点的结构体指针变量 */
	slqueuelink p;
	/* 1. 判断链式队列是否存在 */
	if(lq == NULL)
	{
		printf("single linked list queue is not existed!\n");
		return -1;
	}
	/* 2. 申请入队节点内存空间 */
	p = (slqueuelink)malloc(sizeof(slqueuenode));
	/* 3. 判断节点是否申请成功 */
	if(p == NULL)
	{
		printf("single linked list queue node malloc failed!\n");
		return -1;
	}
	/* 4. 初始化新申请的节点 */
	p->data = value;
	p->next = NULL;
	/* 5. 尾部插入节点实现入队 */
	lq->rear->next = p;
	lq->rear = p;/* 尾节点指针移动，p 成为新的尾节点 */
	
	return 0;
}

3.3出队

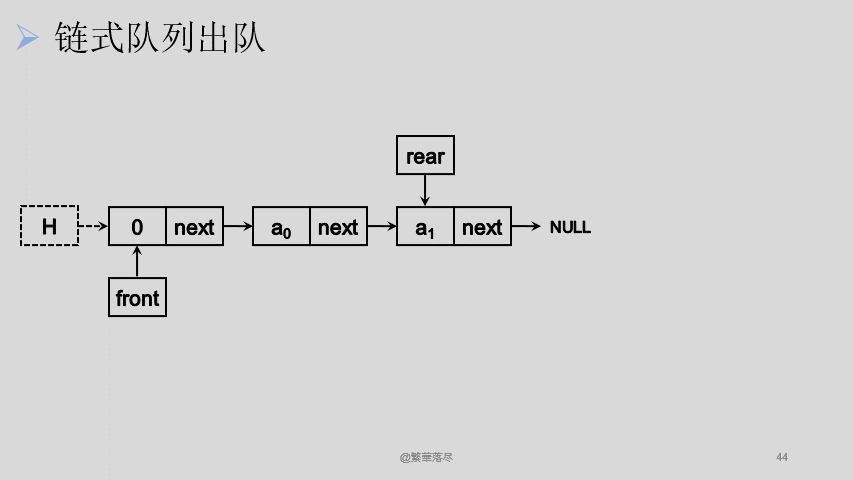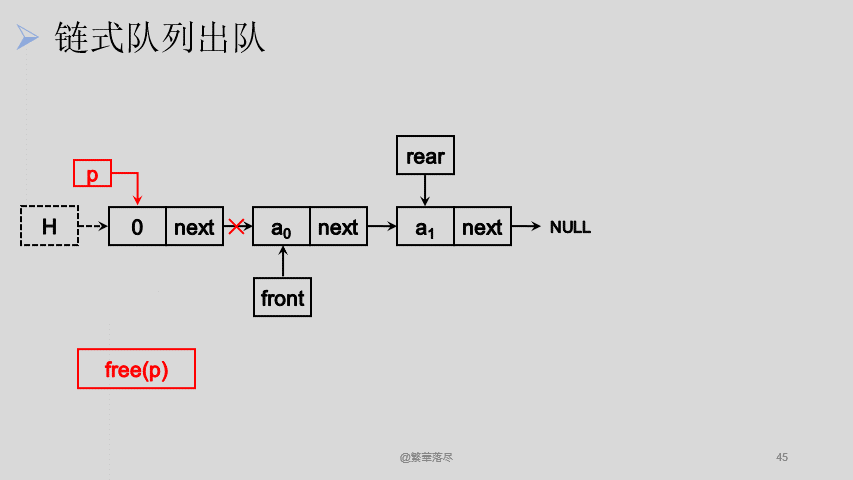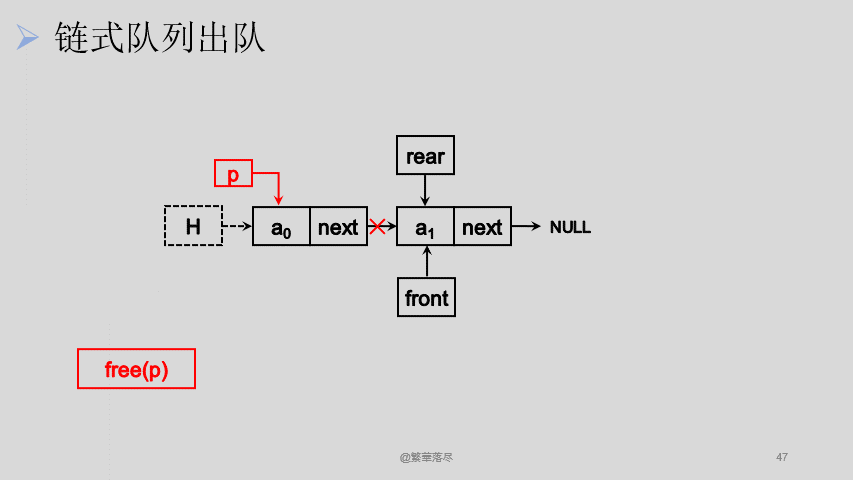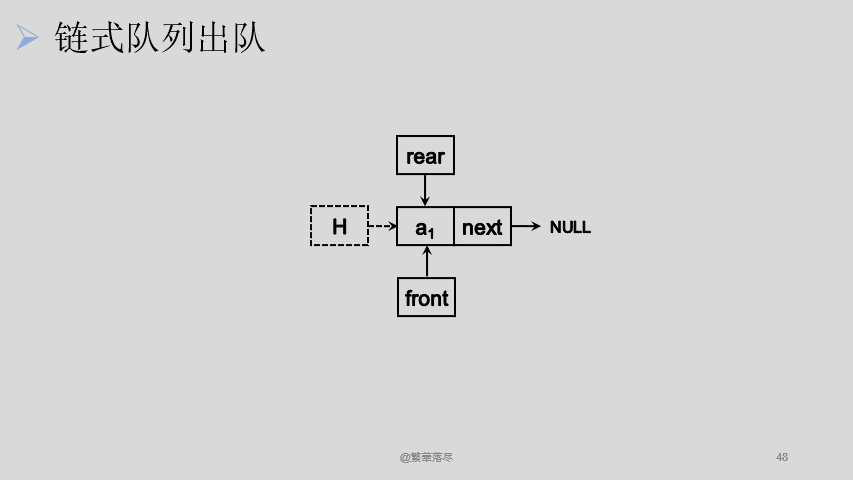
我们将从链表头位置出队，由于我们创建的链表是有头节点的，头节点仅仅是代表这个队列的地址，所以每一次出队我们表面上是将数据出队，实际上这个数据还存在于出队后的头节点中，释放的空间也是出队前头节点的空间：

5

【注意】这里出队的时候不要做队列是否存在以及是否为空的判断，这两个判断若是有返回值的话程序会认为返回值就是出队的元素，所以队列的存在性以及是否为空，要在使用出队函数前进行判断。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * @Function: slqueue_dequeue
 * @Description: 链式队列出队
 * @param lq: 链式队列地址
 * @return  : 返回一个出队的元素
 *            0,入队成功;
 *            -1,链式队列不存在或者新建节点失败
 */
data_t slqueue_dequeue(slqueue_lq *lq) 
{
	/* 定义一个链式队列节点的结构体指针变量 */
	slqueuelink p;
	/* 1. 判断链式队列是否存在 */
	/* 此步骤需要在函数外判断，因为这里返回的话，会认为返回值是出队的数据 */
	/* 2. 判断链式队列是否为空 */
	/* 此步骤需要在函数外判断，因为这里返回的话，会认为返回值是出队的数据 */
	/* 3. 出队 */
	p = lq->front;
	lq->front = p->next;/* 下一个节点将成为头指针 */
	/* 3. 释放出队的节点的上一个节点空间 */
	free(p);
	p = NULL;
	
	return (lq->front->data);
}

3.4释放

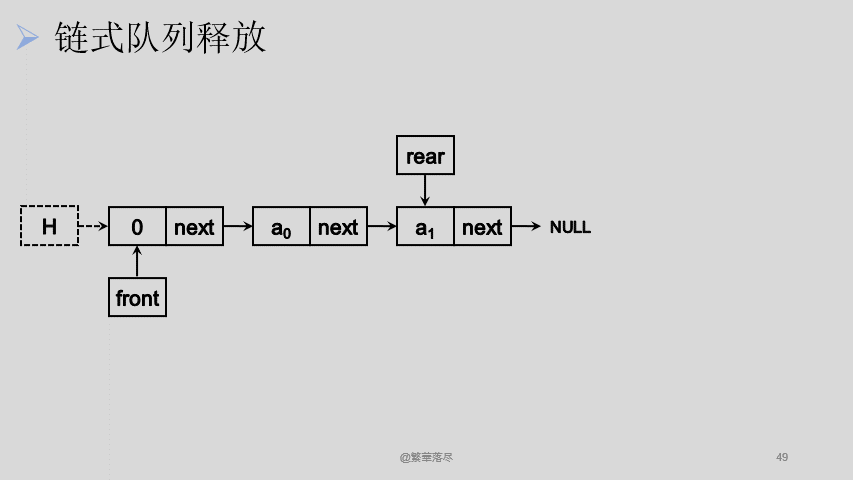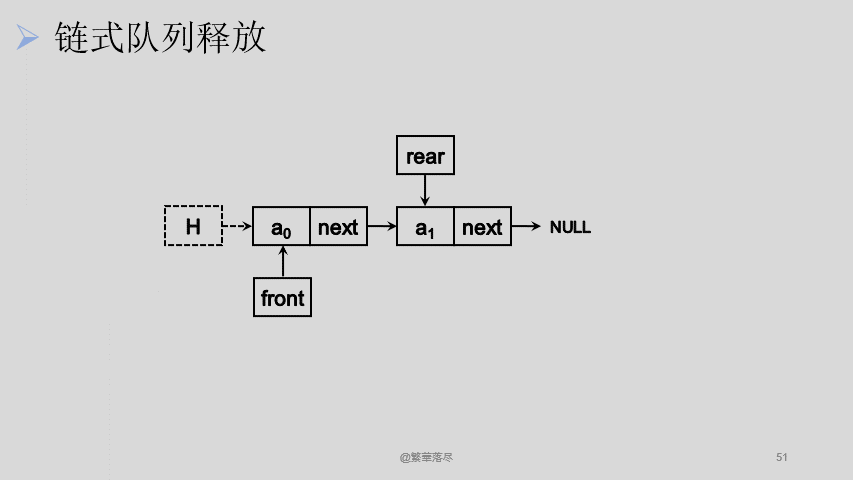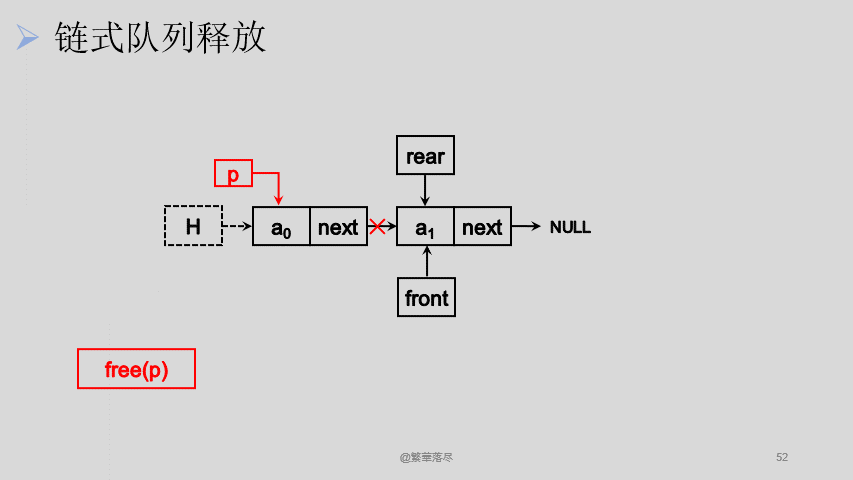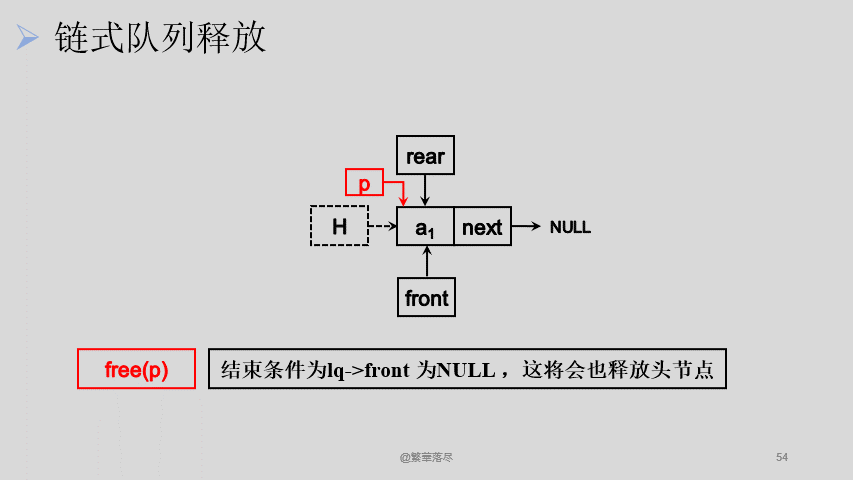
释放的方式与出队一样，只是需要将所有节点出队，并且释放掉最后一个头节点，如下图所示：

6
点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * @Function: slqueue_free
 * @Description: 链式队列释放
 * @param lq: 链式队列地址
 * @return  : 返回一个NULL
 *            NULL,释放完成
 */
slqueue_lq * slqueue_free(slqueue_lq *lq) 
{
	/* 定义一个链式队列节点的结构体指针变量 */
	slqueuelink p;
	/* 1. 判断链式队列是否存在 */
	if(lq == NULL)
	{
		printf("single linked list queue is not existed!\n");
		return NULL;
	}
	/* 2. 释放所有节点空间 */
	printf("single linked list queue free:");
	while(lq->front)
	{
		p = lq->front;
		lq->front = p->next;/* 下一个节点成为新的头节点 */
		printf("%d ", p->data);
		free(p);
	}
	puts("");
	/* 3. 释放链式队列的内存空间(front和rear指针) */
	free(lq);
	lq = NULL;
	
	return NULL;
}

3.5清空

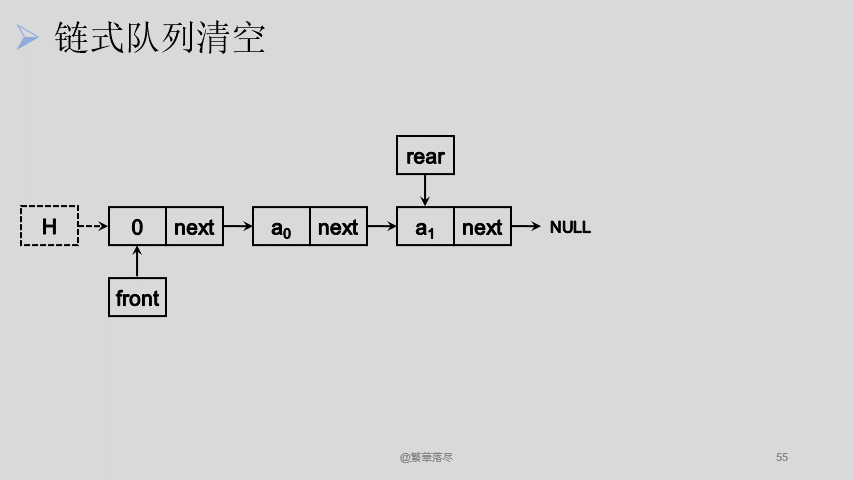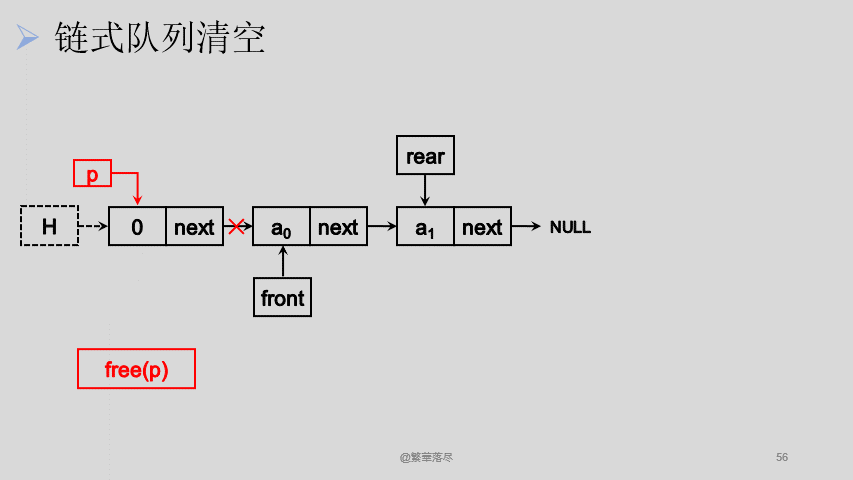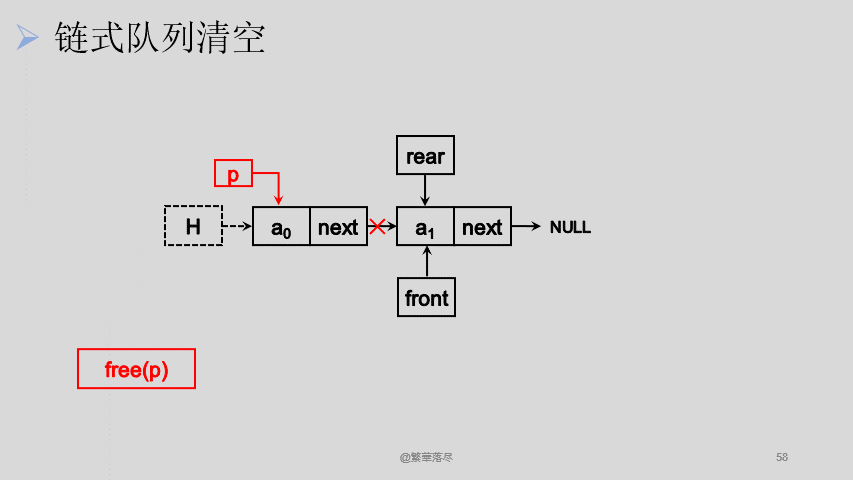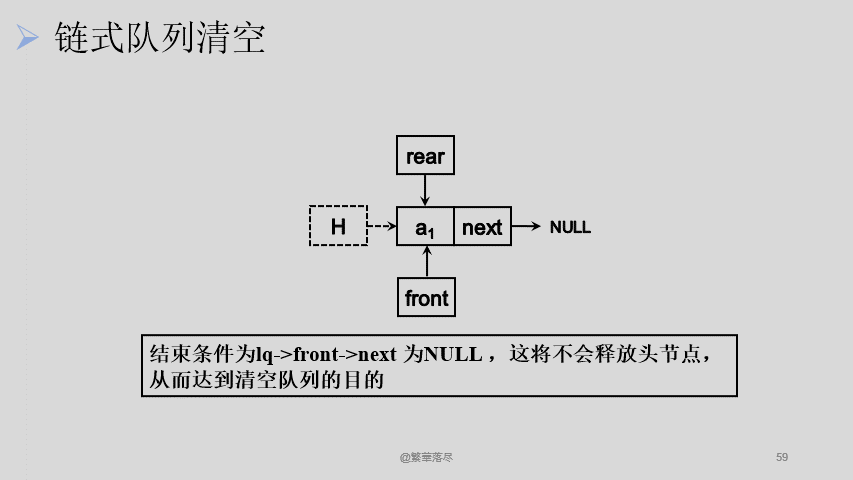
清空的过程，也是将所有节点出队，只不过不释放最后一个节点：

7
点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * @Function: slqueue_clear
 * @Description: 链式队列清空
 * @param lq: 链式队列地址
 * @return  : 返回一个数值
 *            0,清空完成;
 *            -1,链式队列不存在
 */
int slqueue_clear(slqueue_lq *lq) 
{
	/* 定义一个链式队列节点的结构体指针变量 */
	slqueuelink p;
	/* 1. 判断链式队列是否存在 */
	if(lq == NULL)
	{
		printf("single linked list queue is not existed!\n");
		return -1;
	}
	/* 2. 清空链式队列 */
	printf("single linked list queue clear free:");
	while(lq->front->next != NULL)/* 结束条件是剩余一个节点 */
	{
		p = lq->front;
		lq ->front = p->next;
		printf("%d ", p->data);
		free(p);
		p = NULL;
	}
	puts("");
	return 0;
}

3.6显示

此函数将显示所有节点的数据，包括头节点。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @Function: slqueue_show
 * @Description: 链式队列所有节点显示(包括头节点)
 * @param lq: 链式队列地址
 * @return  : 返回一个数值
 *            0,显示完成;
 *            -1,链式队列不存在
 */
int slqueue_show(slqueue_lq *lq) 
{
	/* 定义一个链式队列节点的结构体指针变量 */
	slqueuelink p;
	/* 1. 判断链式队列是否存在 */
	if(lq == NULL)
	{
		printf("single linked list queue is not existed!\n");
		return -1;
	}
	/* 2. 遍历链式队列 */
	p = lq->front;
	printf("single linked list queue:");
	while(p != NULL)
	{
		printf("%d ", p->data);
		p = p->next;
	}
	puts("");
	return 0;
}

3.7判空

此函数将显示所有节点的数据，包括头节点。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @Function: slqueue_empty
 * @Description: 链式队列是否为空
 * @param lq: 链式队列地址
 * @return  : 返回一个数值
 *            0,链式队列非空;
 *            1,链式队列为空;
 *            -1,链式队列不存在
 */
int slqueue_empty(slqueue_lq *lq) 
{
	/* 1. 判断链式队列是否存在 */
	if(lq == NULL)
	{
		printf("single linked list queue is not existed!\n");
		return -1;
	}
	/* 2. 判断front和rear是否相等 */
	if(lq->front == lq->rear)
		return 1;
	else
		return 0;
	/* 或者可以写成下边的情况 */
	// return (lq->front == lq->rear ? 1 : 0);
}