LV03-08-数据结构-栈

发表于 分类于 ， ， 本文字数： 3.7k 阅读时长 ≈ 13 分钟

本文主要是数据结构——栈的相关笔记，若笔记中有错误或者不合适的地方，欢迎批评指正😃。

点击查看使用工具及版本
Windows windows11
Ubuntu Ubuntu16.04的64位版本
VMware® Workstation 16 Pro 16.2.3 build-19376536
SecureCRT Version 8.7.2 (x64 build 2214) - 正式版-2020年5月14日
开发板 正点原子 i.MX6ULL Linux阿尔法开发板
uboot NXP官方提供的uboot，NXP提供的版本为uboot-imx-rel_imx_4.1.15_2.1.0_ga(使用的uboot版本为U-Boot 2016.03)
linux内核 linux-4.15(NXP官方提供)
STM32开发板 正点原子战舰V3(STM32F103ZET6)
点击查看本文参考资料
参考方向 参考原文
------
点击查看相关文件下载
--- ---

一、栈的概念

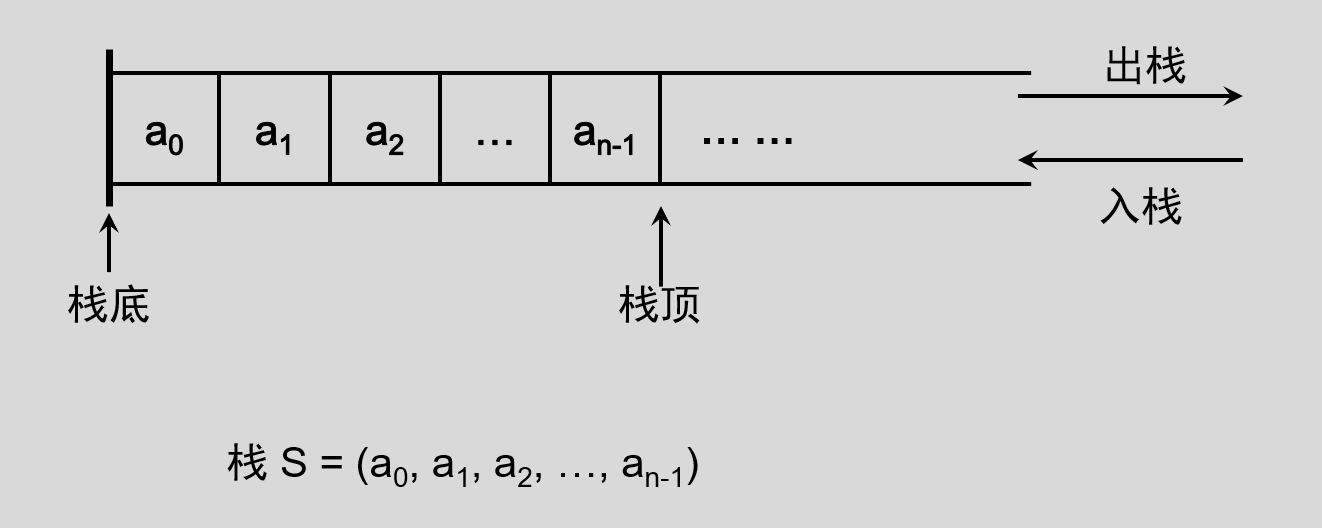
栈是限制在一端进行插入操作和删除操作的线性表（俗称堆栈）。

  • 栈顶：允许进行操作的一端称为栈顶。

  • 栈底：另一固定端称为栈底。

  • 空栈：没有元素的栈称为空栈。

  • 出栈：栈中提取出指定元素，此过程被称为出栈（或弹栈）。

  • 入栈：向栈中添加元素，此过程被称为进栈（入栈或压栈）。

根据栈的定义，可以想象，水杯可以想象为一个栈，接水的时候相当于元素入栈，倒水的时候相当于元素出栈，没有水的时候就相当于空栈。

栈的特点是后进先出（ LIFO ），它是一种特殊的线性存储结构，顺序结构和链式结构都可以实现栈，使用顺序结构实现的栈称为顺序栈，使用链式结构实现的栈称为链式栈。两种实现方式的区别仅限于数据元素在实际物理空间上存放的相对位置，顺序栈底层采用的是数组，链栈底层采用的是链表。

image-20220430092434203

二、顺序栈

1.存储结构

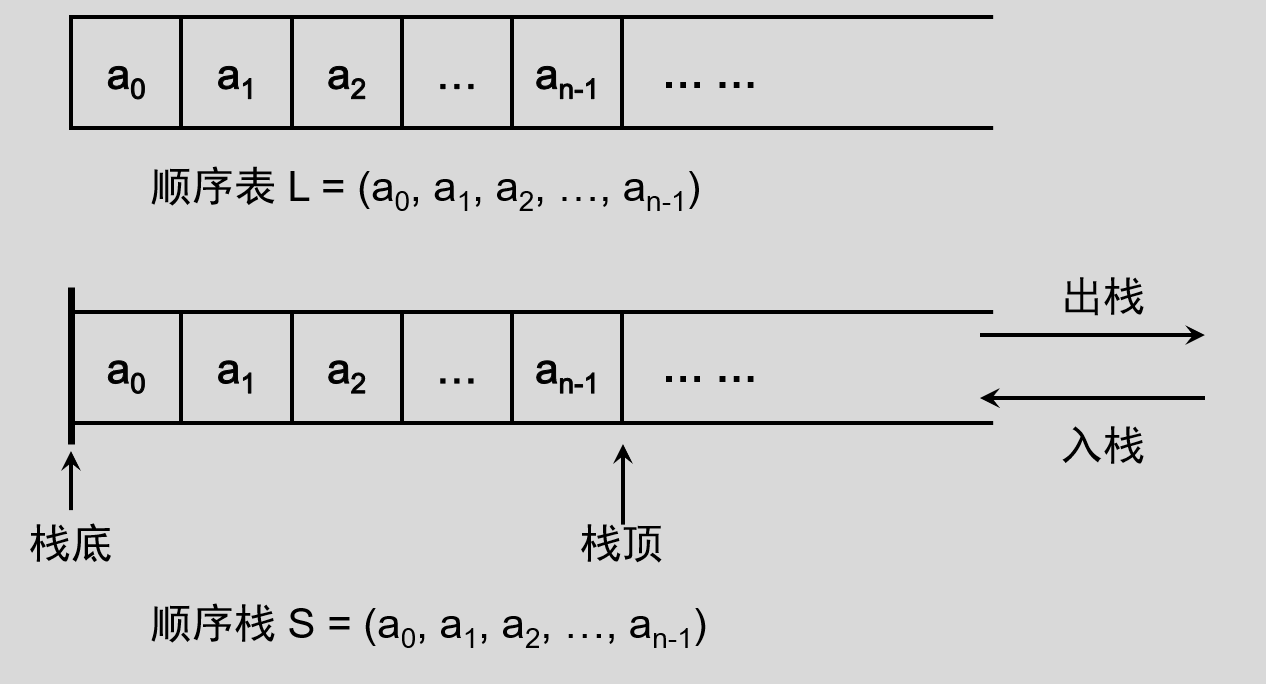
顺序栈，即用顺序表实现栈存储结构。顺序表（底层实现是数组）和栈的存储数据的方式非常想似，只不过栈对数据的存取过程有特殊的限制，而顺序表没有。

image-20220430092600384

2.结构体实现

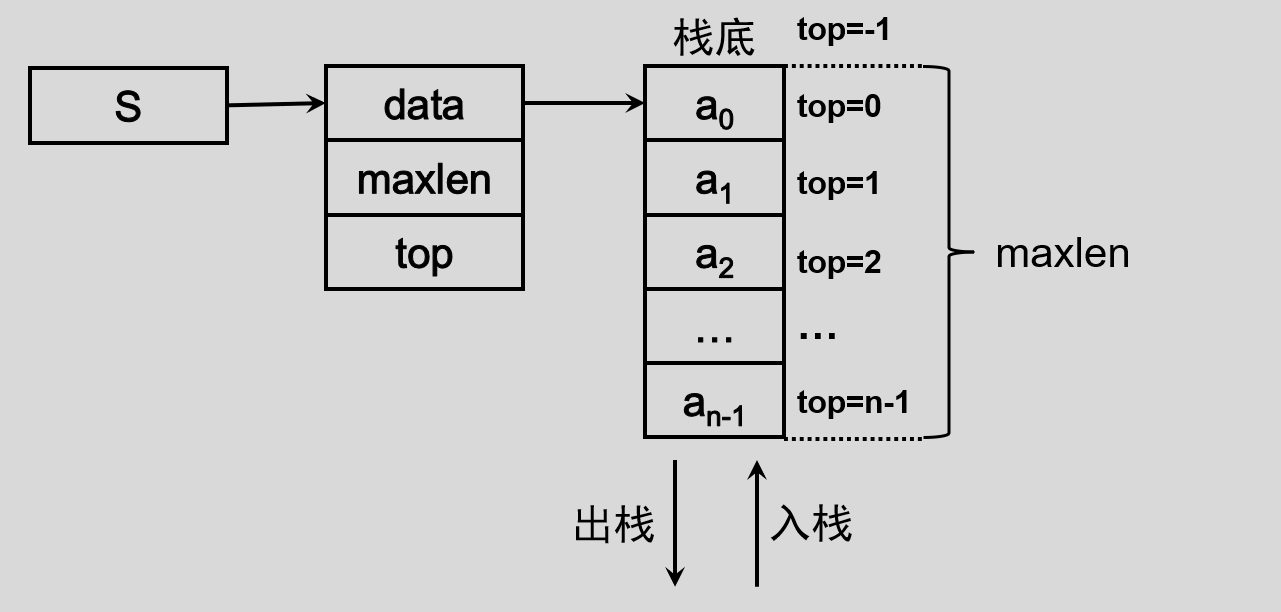
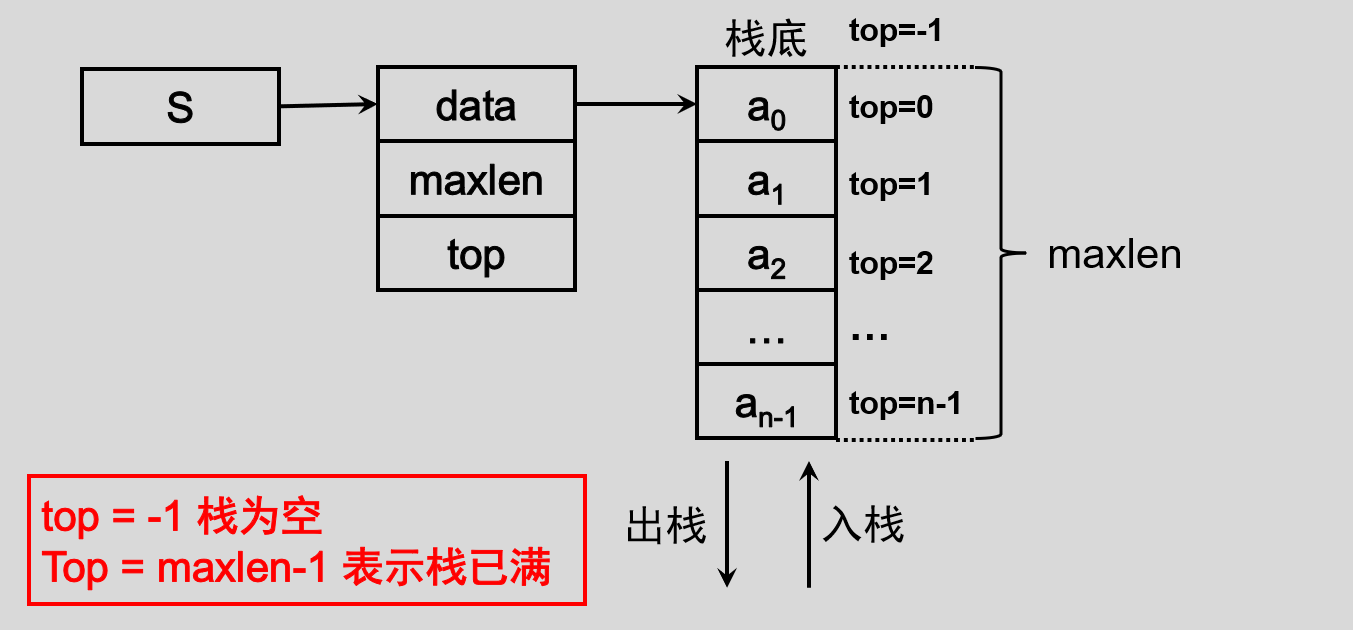
可以把顺序栈看做是顺序表的一种，具有顺序表同样的存储结构，由数组定义，配合用数组下标表示的栈顶指针 top （相对指针）完成各种操作。顺序栈数据类型定义的 C 语言实现如下：

1
2
3
4
5
6
7
8
typedef int data_t; /* 定义栈中数据元素的数据类型 */

typedef struct 
{
	data_t *data;  /* 用指针指向栈的存储空间 */
	int maxlen;    /* 当前栈的最大元素个数 */
	int top;       /* 指示栈顶位置(数组下标)的变量 */
}seqstack;         /* 顺序栈类型定义 */

3.顺序栈基本操作

相关的源代码可以在这里下载：

数据结构 栈 (密码:du8k)

3.1创建顺序栈

image-20220430094437528
点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * @Function: seqstack_create
 * @Description: 顺序栈创建
 * @param len: 顺序栈的最大长度 
 * @return  : 返回一个地址
 *            NULL,创建失败;
 *            other,创建成功
 */
seqstack * seqstack_create(int len) 
{
	/* 定义一个顺序栈结构体变量 */
	seqstack * S;
	/* 1.申请栈空间 */
	if ((S =(seqstack *)malloc(sizeof(seqstack))) == NULL) 
	{
		printf("seqstack malloc failed!\n");
		return NULL;
	}
	/* 2.申请栈中元素数据空间 */
	if ((S->data = (data_t *)malloc(len * sizeof(data_t)))==NULL) 
	{
		printf("seqstack data malloc data failed！\n");
		free(S); /* 申请失败后，释放前边申请的栈空间 */
		return NULL;
	}
	
	/* 3.申请的内存空间位于堆上，需要进行初始化 */
	memset(S->data, 0, len * sizeof(data_t));
	S->maxlen = len;
	S->top = -1;

	return S;
}

3.2栈状态检测

image-20220430094855574

3.2.1栈是否为空

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @Function: seqstack_empty
 * @Description: 顺序栈是否为空
 * @param s : 顺序栈地址
 * @return  : 返回一个数值
 *            0,顺序栈非空;
 *            1,顺序栈为空;
 *            -1,顺序栈不存在
 */
int seqstack_empty(seqstack * S)
{
	/* 1.判断栈空间是否存在 */
	if (S == NULL) 
	{
		printf("seqstack is not existed!\n");
		return -1;
	}
	
	/* 2.判断栈的状态 */
	if(S->top == -1) 
		return 1;
	else
		return 0;
	/* 或者写成下边的 */
	//return (s->top == -1 ? 1 : 0); 
}

3.2.2栈是否已满

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * @Function: seqstack_full
 * @Description: 顺序栈是否已满
 * @param s : 顺序栈地址
 * @return  : 返回一个数值
 *            0,顺序栈未满;
 *            1,顺序栈已满;
 *            -1,顺序栈不存在
 */
int seqstack_full(seqstack * S)
{
	/* 1.判断栈空间是否存在 */
	if (S == NULL) 
	{
		printf("seqstack is not existed!\n");
		return -1;
	}
	
	/* 2.判断栈的状态 */
	if(S->top == S->maxlen-1) 
		return 1;
	else
		return 0;
	/* 或者写成下边的 */
	//return (s->top == -1 ? 1 : 0); 
}

3.3数据入栈

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * @Function: seqstack_push
 * @Description: 入栈
 * @param S : 顺序栈地址
 * @param value : 要入栈的数据
 * @return  : 返回一个数值
 *            0,释放成功;
 *            -1,顺序栈不存在或者栈已满
 */
int seqstack_push(seqstack * S, data_t value) 
{
	/* 1.判断栈空间是否存在 */
	if (S == NULL) 
	{
		printf("seqstack is not existed!\n");
		return -1;
	}
	/* 2.判断栈空间是否已满 */
	if (S->top == S->maxlen-1) 
	{
		printf("seqstack is full!\n");
		return -1;
	}
	/* 3.更新数据 */
	S->top++;
	S->data[S->top] = value;

	return 0;
}

3.4数据出栈

【注意】这里出栈的时候不要做栈是否存在以及是否为空的判断，这两个判断若是有返回值的话程序会认为返回值就是出栈的元素，所以栈的存在性以及是否为空，要在使用出栈函数前进行判断。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * @Function: seqstack_push
 * @Description: 出栈
 * @param S : 顺序栈地址
 * @return  : 返回一个栈中数据
 */
data_t seqstack_pop(seqstack * S) 
{
	/* 1. 判断栈空间为否为空 */
	/* 这一步不需要，因为栈中元素可能是任意数值，所以这里做判断并不合适，需要在函数外判断 */
	/* 2. 数据出栈 */
	S->top--;
	return (S->data[S->top+1]);
}

3.5清空栈

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * @Function: seqstack_clear
 * @Description: 顺序栈清空
 * @param s : 顺序栈地址
 * @return  : 返回一个数值
 *            0,顺序栈清空成功;
 *            -1,顺序栈不存在
 */
int seqstack_clear(seqstack * S)
{
	/* 1.判断栈空间是否存在 */
	if (S == NULL) 
	{
		printf("seqstack is not existed!\n");
		return -1;
	}
	
	/* 2.清空栈，可以说是认为没有数据，那么它就没有数据 */
	S->top = -1; 
	return 0;
}

3.6释放顺序栈

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @Function: seqstack_free
 * @Description: 释放顺序栈空间及数据空间
 * @param S : 顺序栈地址
 * @return  : 返回一个数值
 *            0,释放成功;
 *            -1,顺序栈不存在 
 */
int seqstack_free(seqstack * S) 
{
	/* 1.判断顺序栈空间是否存在 */
	if (S == NULL) 
	{
		printf("seqstack is not existed!\n");
		return -1;
	}
	/* 2.释放顺序栈中所有元素空间 */
	if (S->data != NULL)
	{
		free(S->data);
	}	
	/* 3.释放顺序栈结构体变量空间 */
	free(S);
	printf("seqstack free completed!\n");

	return 0;
}

3.7显示顺序栈

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * @Function: seqstack_show
 * @Description: 顺序栈数据显示
 * @param s : 顺序栈地址
 * @return  : 返回一个数值
 *            0,顺序栈显示成功;
 *            -1,顺序栈不存在或者顺序栈为空
 */
int seqstack_show(seqstack * S)
{
	int i = 0;
	/* 1.判断栈空间是否存在 */
	if (S == NULL) 
	{
		printf("seqstack is not existed!\n");
		return -1;
	}
	/* 2. 判断顺序栈是否为空 */
	if (S->top == -1) 
	{
		printf("seqstack is empty!\n");
		return -1;
	}
	/* 2. 显示顺序栈元素 */
	printf("seqstack: ");
	while(i <= S->top)
	{
		printf("%d ", S->data[i]);
		i++;
	}
	puts("");
	 
	return 0;
}

三、链式栈

1.存储结构

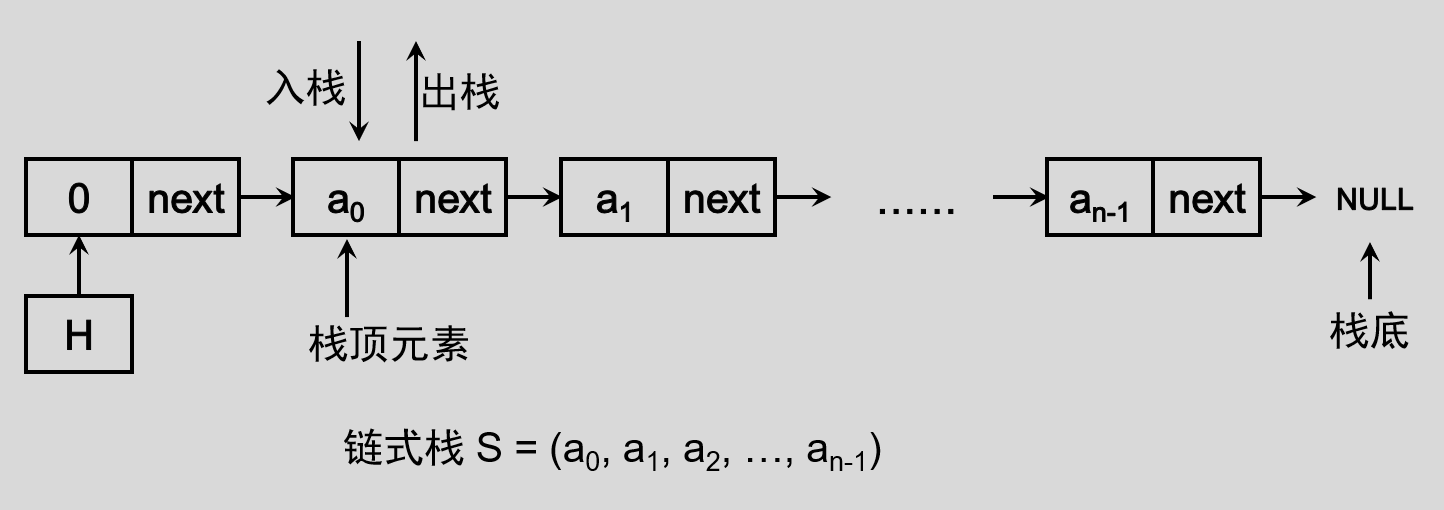
当我们固定单链表的一端，只在一段进行操作，便构成了栈，我们可以将链表头部作为栈顶的一端，这样可以避免在实现数据入栈”和 出栈 操作时做大量遍历链表的耗时操作。

image-20220430134519127

这样就意味着我们需要在头节后进行节点的插入和删除来完成入栈和出栈。

2.结构体实现

我们通过单链表来实现栈，这样其实它还是一个单链表，仅仅是限制了插入和删除节点的位置罢了，所以结构体可以像这样定义：

1
2
3
4
5
6
7
typedef int data_t; /* 定义栈中数据元素的数据类型 */

typedef struct slstack_node 
{
	data_t data;
	struct slstack_node *next;
}slstacknode, * slstacklink;

3.链式栈的基本操作

相关的源代码可以在这里下载：

数据结构 栈 (密码:du8k)

3.1链栈创建

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * @Function: slstack_create
 * @Description: 链式栈创建
 * @param   : none
 * @return  : 返回一个地址
 *            NULL,创建失败;
 *            other,创建成功
 */
slstacklink slstack_create()
{
	/* 定义一个链式栈的结构体指针变量 */
	slstacklink S;
	/* 1. 申请链式栈的内存空间 */
	S = (slstacklink)malloc(sizeof(slstacknode));
	/* 2. 判断是否申请成功 */
	if(S == NULL)
	{
		printf("slinked list stack malloc failed!\n");
		return NULL;
	}
	/* 3.初始化内存空间 */
	S->data = 0;
	S->next = NULL;
	
	return S;
}

3.2链栈释放

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @Function: slstack_free
 * @Description: 链式栈释放
 * @param S : 链式栈地址
 * @return  : 返回一个NULL
 *            NULL,释放完成
 */
slstacklink slstack_free(slstacklink S)
{
	/* 定义一个链式栈的结构体指针变量 */
	slstacklink p;
	/* 1. 判断链式栈是否存在 */
	if (S == NULL) 
	{
		printf("slinked stack is not existed!\n");
		return NULL;
	}
	/* 2. 释放各个节点空间 */
	printf("slinked stack free:");
	while(S != NULL)
	{
		p = S;
		printf("%d ", p->data);
		S = S->next;
		free(p);
	}
	puts("");
	
	return NULL;
}

3.3链栈显示

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * @Function: slstack_show
 * @Description: 链式栈数据显示
 * @param S : 链式栈地址
 * @return  : 返回一个数值
 *            0,显示成功;
 *            -1,链式栈不存在
 */
int slstack_show(slstacklink S)
{
	/* 定义一个链式栈的结构体指针变量 */
	slstacklink p;
	/* 1. 判断链式栈是否存在 */
	if (S == NULL) 
	{
		printf("slinked stack is not existed!\n");
		return -1;
	}
	/* 2. 判断链式栈是否为空 */
	if (S->next == NULL) 
	{
		printf("slinked stack is empty!\n");
		return -1;
	}
	/* 3. 遍历所有节点 */
	p = S;
	printf("slinked stack:");
	while(p->next != NULL)
	{
		printf("%d ", p->next->data);
		p = p->next;
	}
	puts("");
	
	return 0;
}

3.4链栈状态

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @Function: slstack_empty
 * @Description: 链式栈是否为空
 * @param S : 链式栈地址
 * @return  : 返回一个数值
 *            0,链式栈非空;
 *            1,链式栈为空;
 *            -1,链式栈不存在
 */
int slstack_empty(slstacklink S)
{
	/* 1. 判断链式栈是否存在 */
	if (S == NULL) 
	{
		printf("slinked stack is not existed!\n");
		return -1;
	}
	/* 2. 判断链式栈头节点后是否有节点 */
	if(S->next == NULL)
		return 1;
	else
		return 0;
	/* 也可以写成下边的形式 */
	// return (S->next == NULL ? 1 : 0);
}

3.5数据入栈

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * @Function: slstack_push
 * @Description: 入栈
 * @param S : 链式栈地址
 * @param value : 要入栈数据
 * @return  : 返回一个数值
 *            0,入栈成功;
 *            -1,入栈失败
 */
int slstack_push(slstacklink S, data_t value)
{
	/* 定义一个链式栈的结构体指针变量 */
	slstacklink p;
	/* 1. 判断链式栈是否存在 */
	if (S == NULL) 
	{
		printf("slinked stack is not existed!\n");
		return -1;
	}
	/* 2. 新建节点并初始化 */
	p = (slstacklink)malloc(sizeof(slstacknode));
	if(p == NULL)
	{
		printf("The new node malloc failed!\n");
		return -1;
	}
	p->data = value;
	p->next = NULL;
	/* 3.头部插入节点 */
	p->next = S->next;
	S->next = p;
	
	return 0;
}

3.6数据出栈

【注意】这里出栈的时候不要做栈是否存在以及是否为空的判断，这两个判断若是有返回值的话程序会认为返回值就是出栈的元素，所以栈的存在性以及是否为空，要在使用出栈函数前进行判断。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @Function: slstack_pop
 * @Description: 出栈
 * @param S : 链式栈地址
 * @return  : 返回一个数值
 *            0,出栈成功;
 *            -1,链式栈不存在或者链式栈为空
 */
data_t slstack_pop(slstacklink S)
{
	/* 定义一个链式栈的结构体指针变量 */
	slstacklink p;
	data_t temp;
	/* 1. 判断链式栈是否存在 */
	/* 这一步不需要，因为栈中元素可能是任意数值，所以这里做判断并不合适，需要在函数外判断 */
	/* 2. 判断链式栈是否为空 */
	/* 这一步不需要，因为栈中元素可能是任意数值，所以这里做判断并不合适，需要在函数外判断 */
	/* 3. 出栈 */
	p = S->next;
	S->next = p->next;
	
	temp = p->data;
	/* 4. 释放出栈节点的内存空间 */
	free(p);
	p = NULL;
	return temp;
}