LV03-11-数据结构-二叉树基础
本文主要是数据结构——二叉树基础知识相关笔记,若笔记中有错误或者不合适的地方,欢迎批评指正😃。
点击查看使用工具及版本
| Windows | windows11 |
| Ubuntu | Ubuntu16.04的64位版本 |
| VMware® Workstation 16 Pro | 16.2.3 build-19376536 |
| SecureCRT | Version 8.7.2 (x64 build 2214) - 正式版-2020年5月14日 |
| 开发板 | 正点原子 i.MX6ULL Linux阿尔法开发板 |
| uboot | NXP官方提供的uboot,NXP提供的版本为uboot-imx-rel_imx_4.1.15_2.1.0_ga(使用的uboot版本为U-Boot 2016.03) |
| linux内核 | linux-4.15(NXP官方提供) |
| STM32开发板 | 正点原子战舰V3(STM32F103ZET6) |
点击查看本文参考资料
| 参考方向 | 参考原文 |
| --- | --- |
1.二叉树定义
什么是二叉树,二叉树也是一种树形结构,它是一种特殊的树,它有以下特点:
(1)二叉树是有序树,严格区分左孩子和右孩子,即使只有一个子节点也要区分左右;
(2)树中包含的各个结点的度不能超过 2 ,只能是 0 、 1 或者 2 。
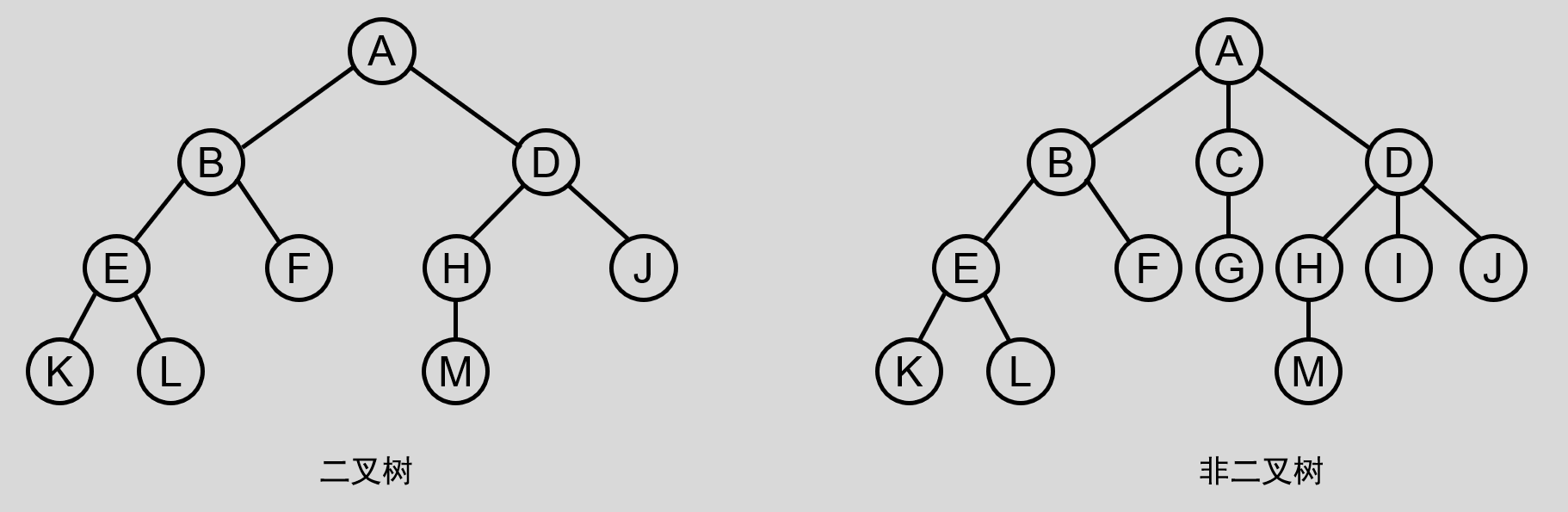
2.二叉树形态
二叉树的形态一共可以有五种:
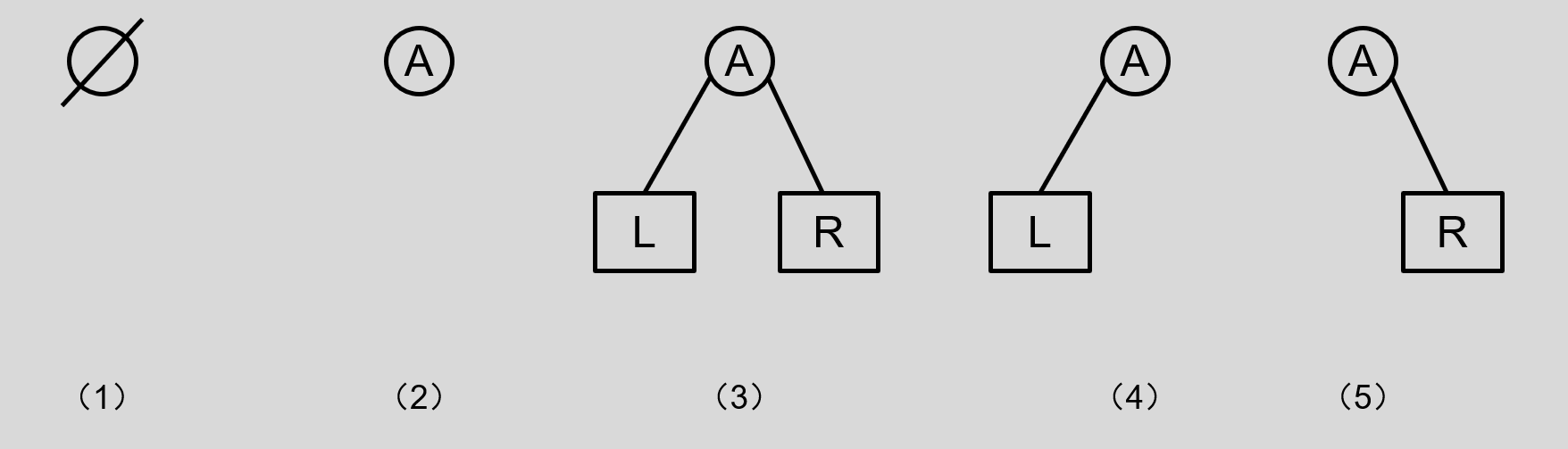
4.二叉树性质
(1)二叉树的第 i (i ≥ 1) 层上至多有$2^{i-1}$个结点。
【证明】数学归纳法:
- i = 1时,只有一个根节点,显然$2^0=1$,上述结论成立;
- 假设对所有的 j ,1 ≤ i <j 时上述结论成立,即在第 j 层上至多有 $2^{j-1}$个结点;
- 所以在第 i - 1 层上至多有$2^{i-2}$个结点,由于二叉树的每个结点的度数至多为 2 ,所以在第 i 层上结点最多为 i - 1层上结点数的两倍,即第 i 层上结点数至多为 $2^{i-1}$。
(2)深度为 k (k ≥ 1) 的二叉树至多有$2^{k}-1$个结点。
【证明】
由性质(1)可知,二叉树第 i 层上至多有 $2^{i-1}$个结点,一共有 k 层,所以总的结点数 n 为:
$n = 2^0 + 2^1 + …… +2^{k-1}$
等比数列求和公式为:$S_n = \frac{a_1-a_nq)}{1-q}$
所以 $ n = \frac{1-2^{k-1}*2}{1-2} = 2^k-1$
(3)对任意的二叉树 T ,若其叶子结点数为$n_0$,度数为 2 的结点数为$n_2$,则$n_0 = n_2 + 1$。
【证明】
设$n_1$为二叉树 T 中度数为 1 的结点数,n 为二叉树的总结点数,则 $n = n_0 + n_1 + n_2$
对于每一个结点来说都是由结点的父结点分支表示的,假设二叉树中树的分支数为 B ,那么总结点数 $n = B + 1$
而二叉树的分支数 $B = n_1 + 2 * n_2$,所以有$n = n_1 + 2*n_2 + 1$
所以$n = n_1 + 2*n_2 + 1 = n_0 + n_1 + n_2 $
两边消去$n_1$可以得到$n_0 = n_2 + 1$。
3.几种二叉树
3.1满二叉树
如果二叉树中除了叶子结点,每个结点的度都为 2 ,则此二叉树称为满二叉树。
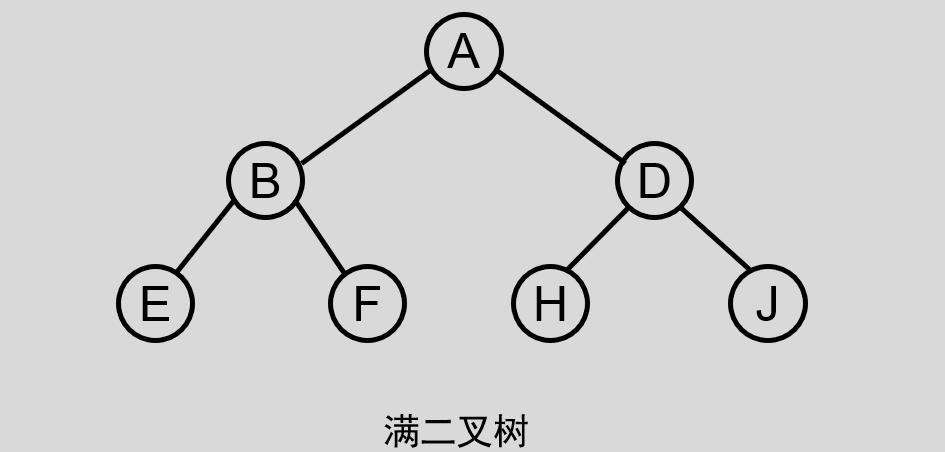
满二叉树除上述三条一般二叉树的性质之外,还有如下性质:
(1)满二叉树的第 i (i ≥ 1) 层上有$2^{i-1}$个结点。
(2)深度为 k (k ≥ 1) 的满二叉树有$2^{k}-1$个结点,叶子数为$2^{k-1}$。
(3)满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
(4)具有 n 个节点的满二叉树的深度为$\log_2(n+1)$。
- 完全二叉树
只有最下面一层有度数小于 2 的节点,且最下面一层的叶节点集中在最左边的若干位置上的二叉树。也就是说完全二叉树去除最下边一层的所有节点后是一个满二叉树。
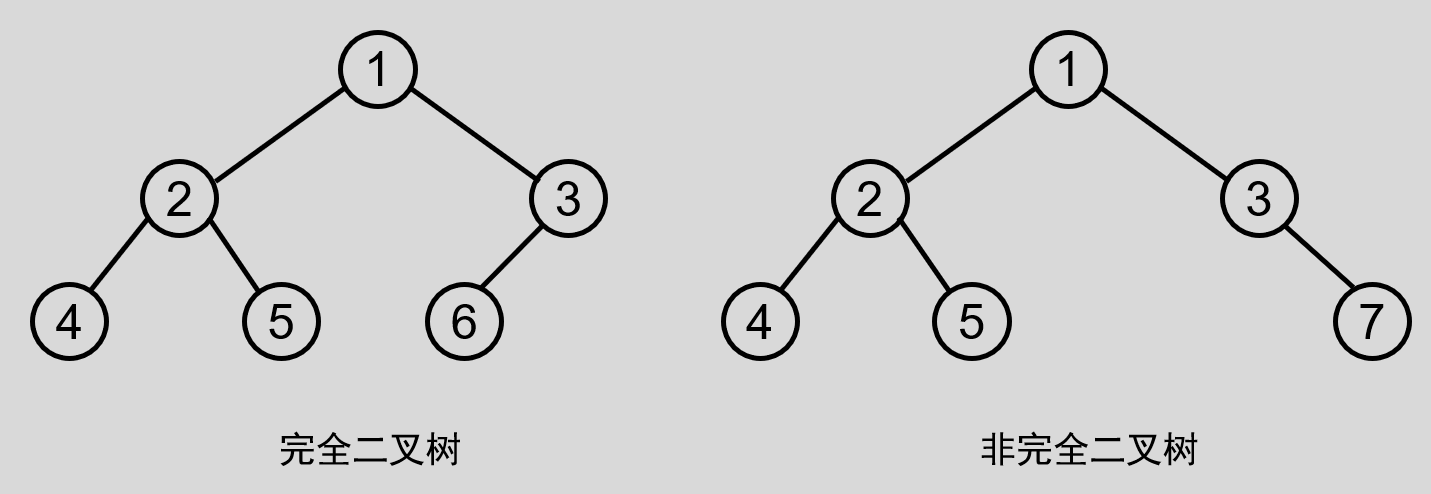
完全二叉树除上述三条一般二叉树的性质之外,还有如下性质:
对于任意一个含有 n 个结点的完全二叉树来说,如果将含有的结点按照层次从左到右依次标号,如上图所示,根节点为 1 号节点,则对任意一个结点 i 有:
(1)当 i > 1 时,结点 i 有父结点,且编号为 i / 2 。
(2)当 2i ≤ n 时,有左孩子,且左孩子编号为 2i ;当 2i > n 时,结点肯定没有左孩子,节点本身为叶子结点。
(3)当 2i + 1 ≤ n 时,有右孩子,且右孩子编号为 2i + 1 ;当 2i + 1 > n 时,结点肯定没有右孩子。
(4)当 i 为奇数且不为 1 时,结点 i 有左兄弟,左兄弟编号为 i - 1 ,否则 i 没有左兄弟。
(5)当 i 为偶数且小于 n 时,结点 i 有右兄弟,右兄弟编号为 i + 1 ,否则 i 没有右兄弟。
4.存储结构
我们前边学的有顺序存储结构和链式存储结构,他们都可以作为二叉树的存储结构。
4.1顺序存储结构
使用顺序表(数组)存储二叉树,这叫做二叉树的顺序存储,但是要注意的就是,顺序存储只适用于完全二叉树。如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
那普通二叉树如何转化为完全二叉树呢?如下图所示:
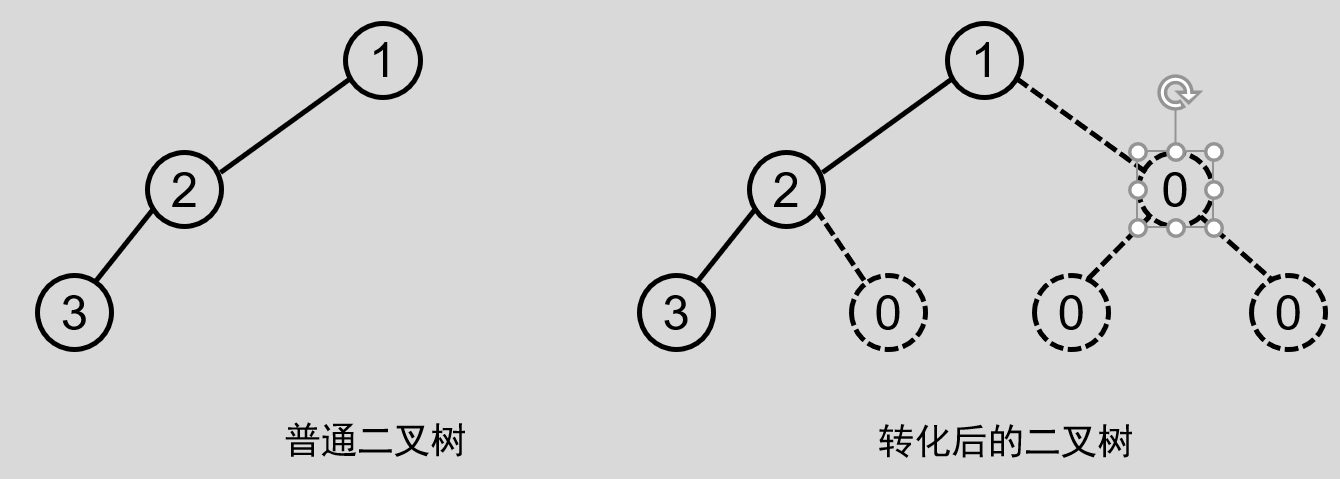
这样一来,二叉树就都可以满足顺序存储的条件了,那怎么存储呢?如下图所示:
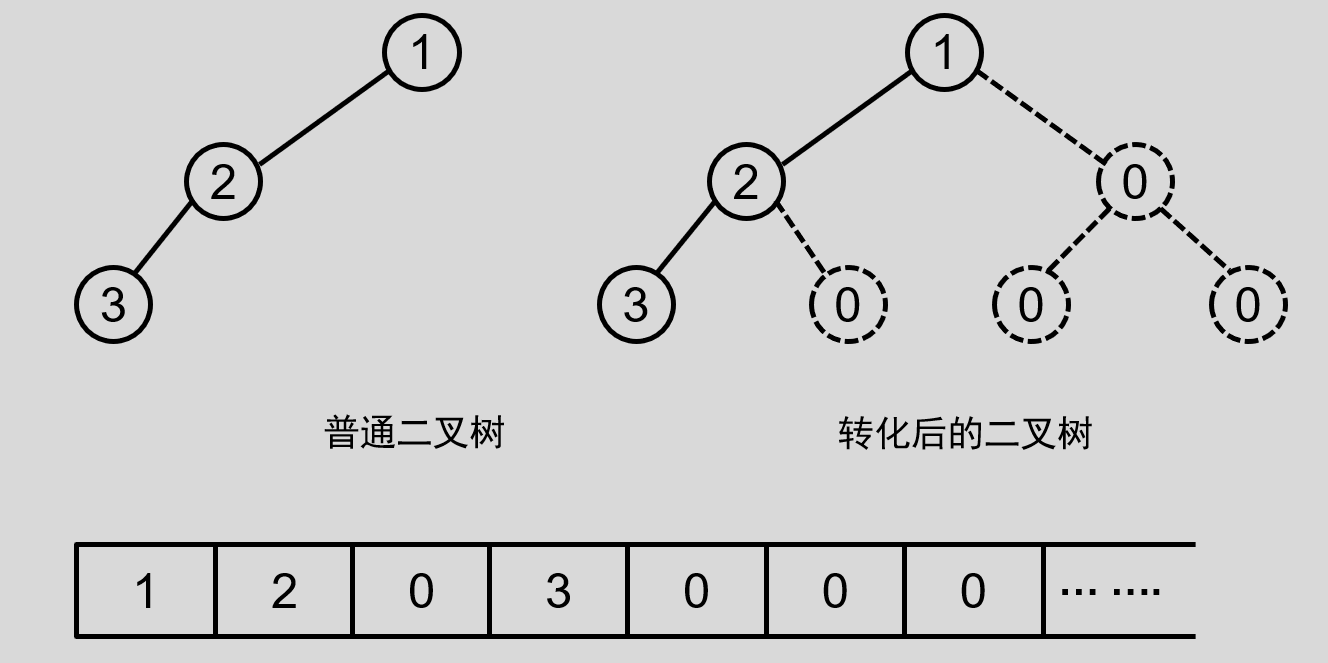
通过顺序表存储的二叉树,可以很轻松还原,但是顺序存储结构是特别浪费空间的,那些为了转化为完全二叉树而补充出来的结点并没有什么实际用处,反而还浪费了很大的空间,比如上图中,原本结点只有三个,但是存储的时候却至少需要多出来三个结点的空间。
4.2链式存储结构
我们还可以通过链表来存放二叉树,存储方式如下:
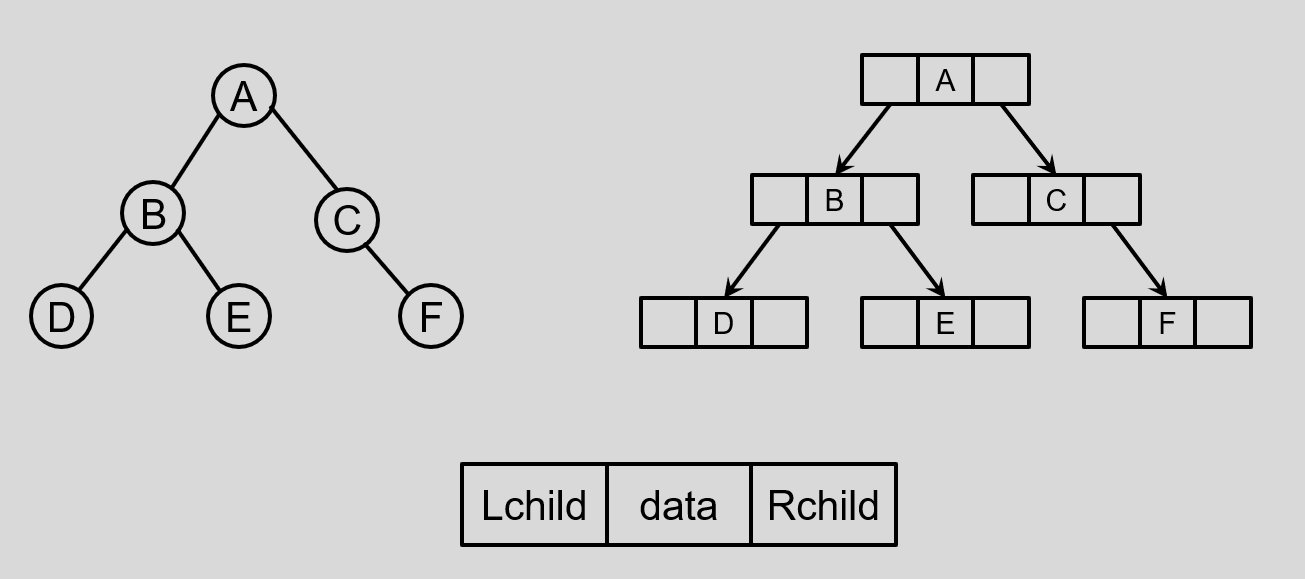
存放结点的链式节点结构有三部分组成:
- Lchild :指针域,指向存放左孩结点的链表节点的指针。
- data :数据域,结点存放的数据。
- Rchild :指针域,指向存放右孩结点的链表节点的指针。
5.二叉树遍历
5.1遍历算法的由来
对于一个二叉树,在我们不知道有哪些遍历算法的情况下,很容易我们会想到一种,就是按层次,从上到下,每一层次从左到右来遍历,这种遍历的方式被称之为层次遍历。
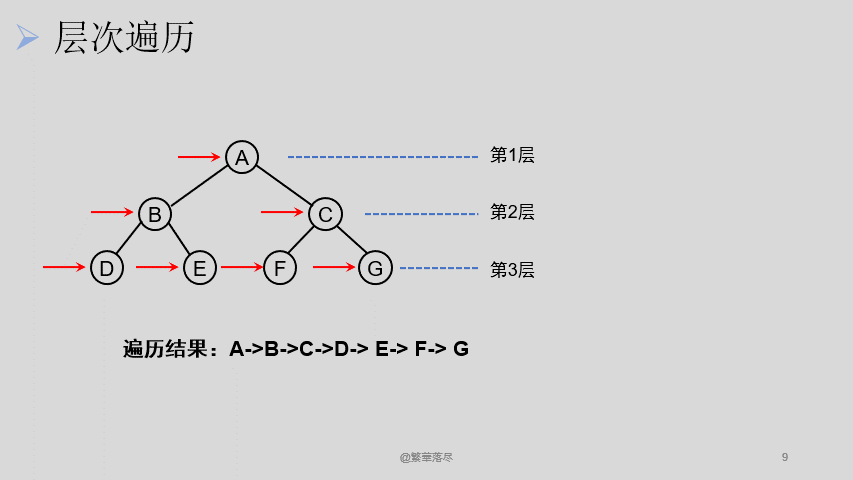
那还有其他的遍历方法吗?还有一种就是我们遵循从上到下,从左到右的遍历方式,如下图所示:
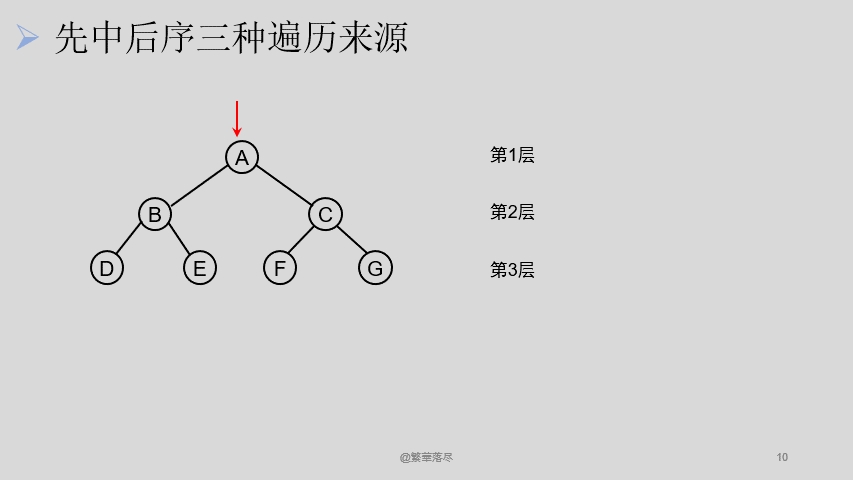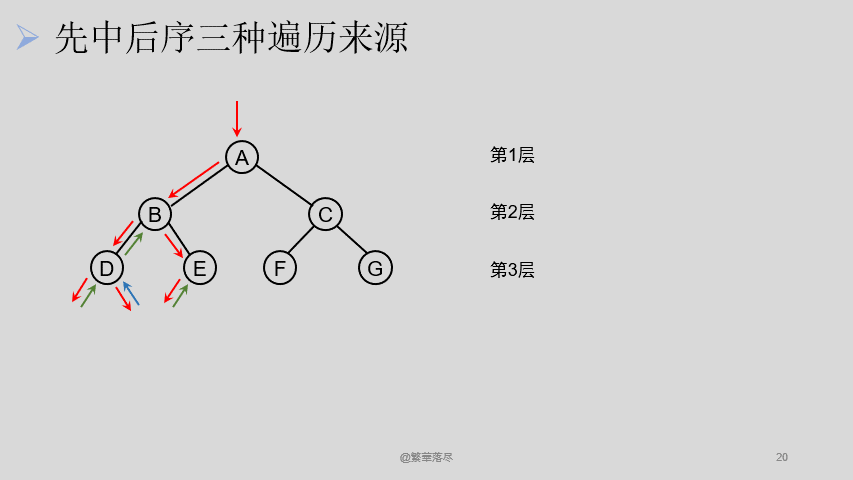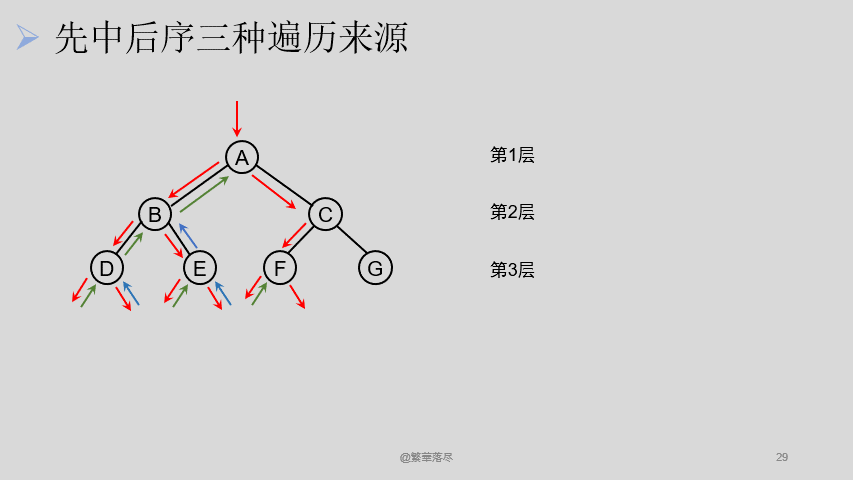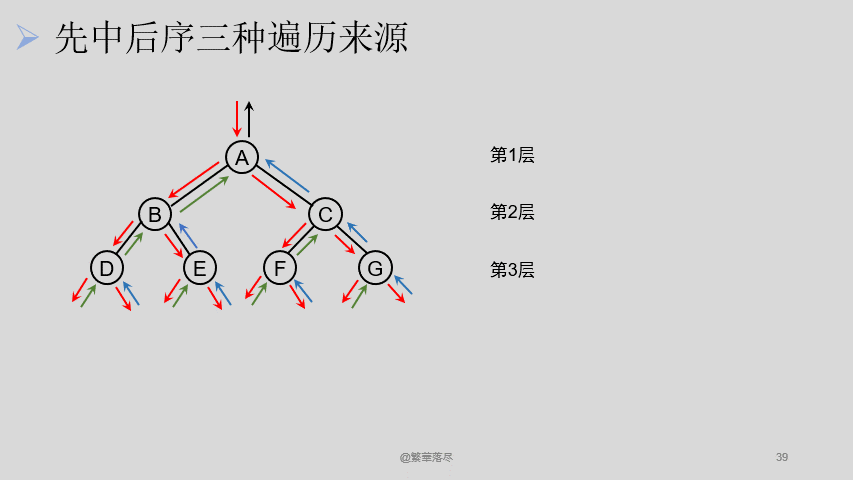
这样依然可以访问到所有的结点,他们的区别是什么呢?层次遍历中,每次只经过结点一次,而下边这种遍历,对于结点 B 来说,遍历的时候经过了它三次,即便是叶子结点,看上去是两次,但是也可以看做是三次。我们可以在经过这个结点不同的时机进行访问,如此便有三种访问方式了:
- 遇到一个结点,先访问,再遍历左右子树,称之为先序遍历。
- 遇到一个结点,第一次先不访问,先访问它的左子树,再访问这个结点,最后访问右子树,称之为中序遍历。
- 遇到一个结点,第一次不访问,先访问左子树,第二次还是不访问,然后访问右子树,最后访问这个结点,称之为后序遍历。
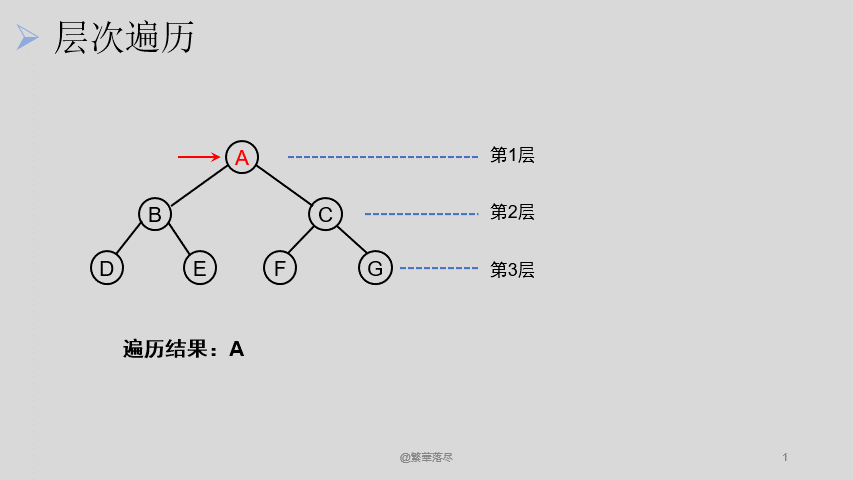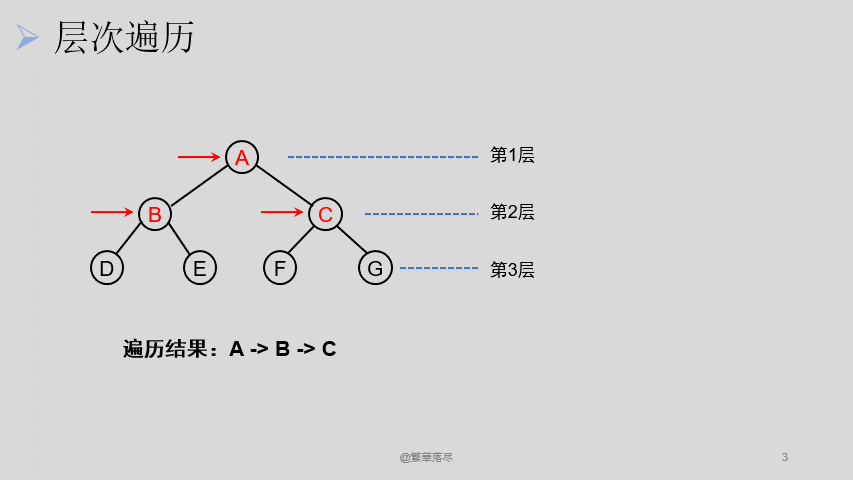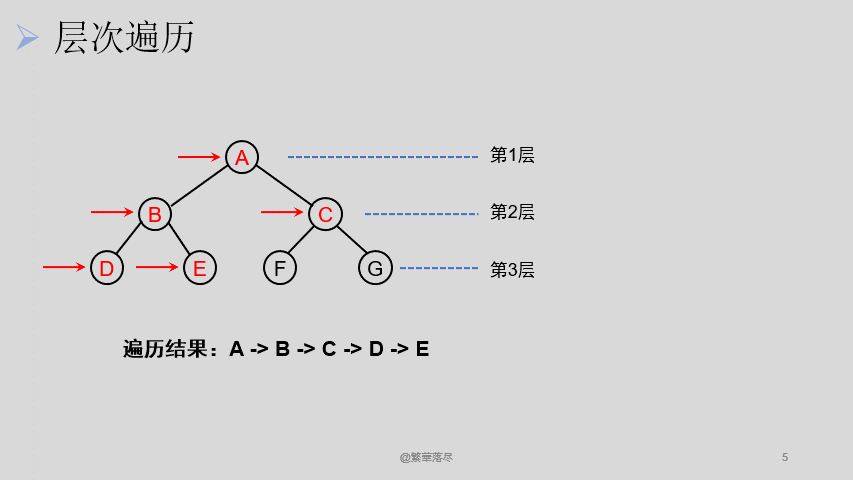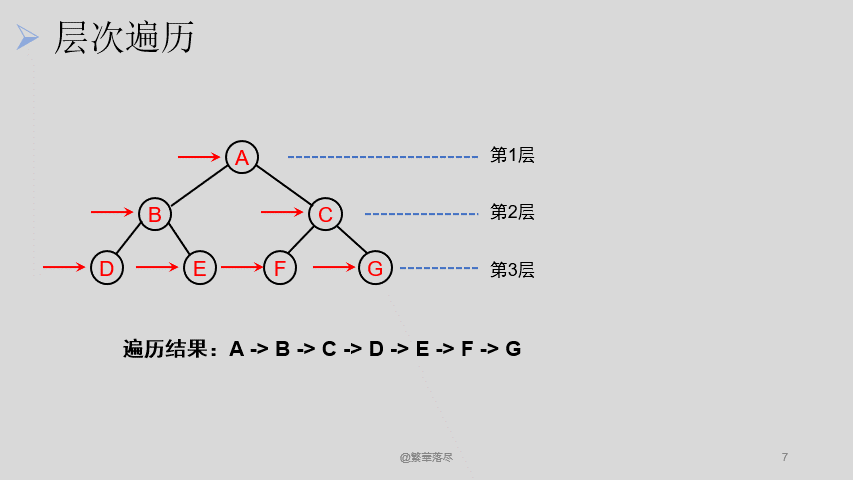
5.2层次遍历
层次遍历过程如下图所示:
5.3先序遍历
先序遍历过程如下图所示:
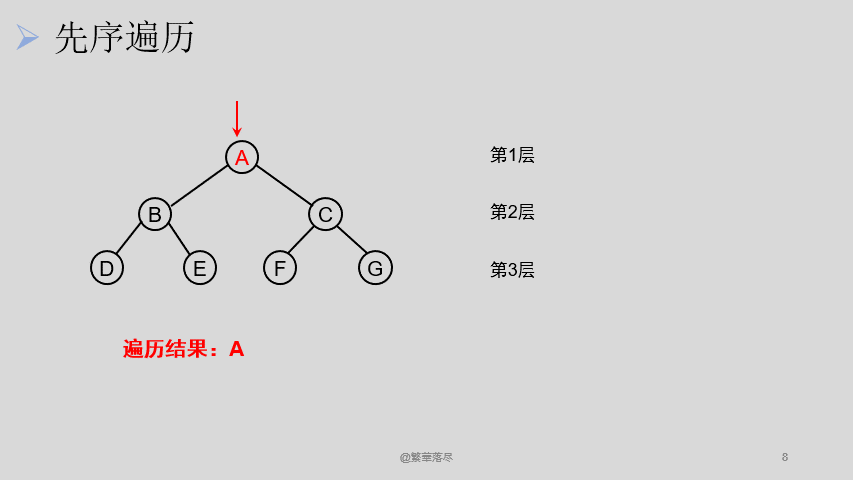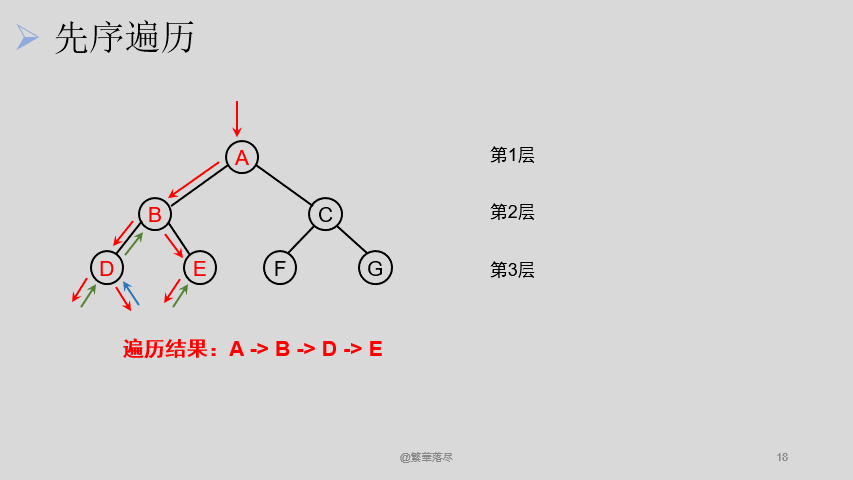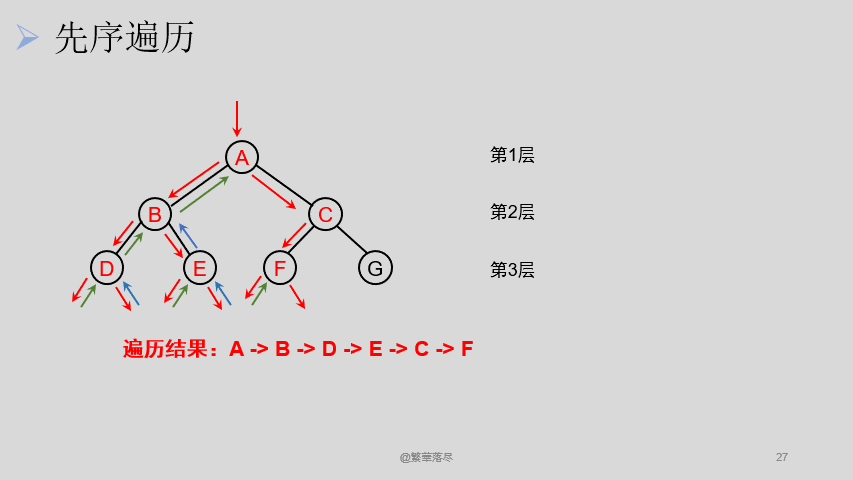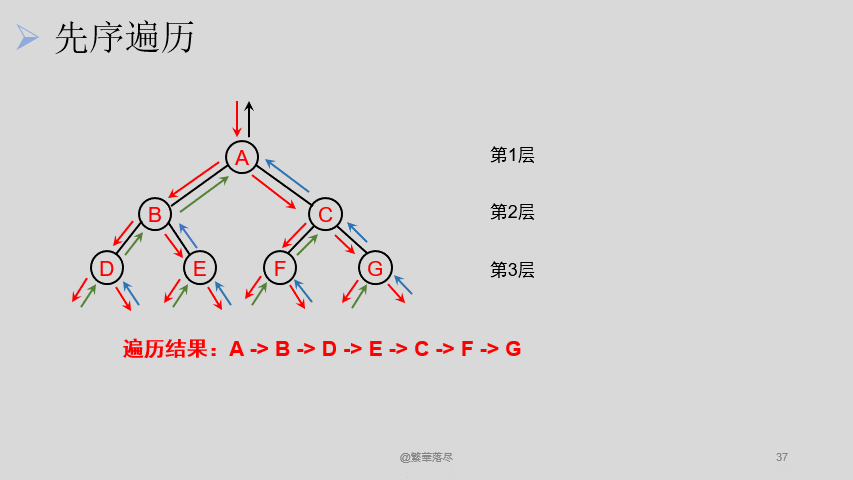
5.4中序遍历
中序遍历过程如下图所示:
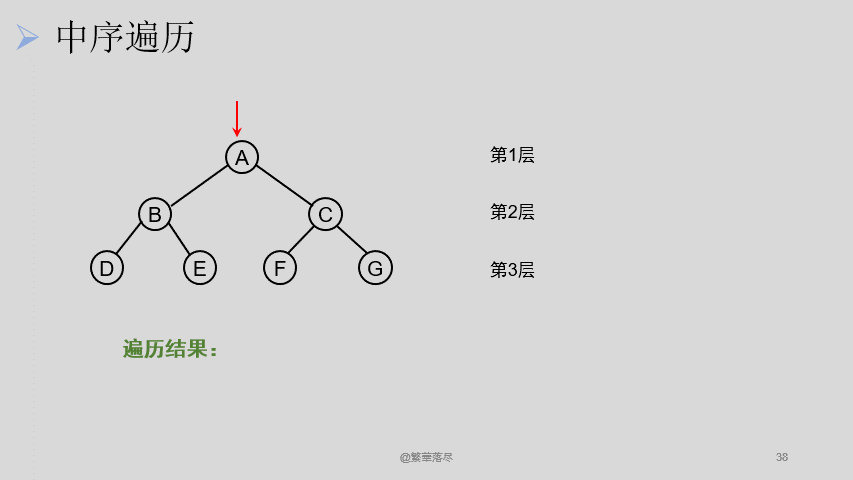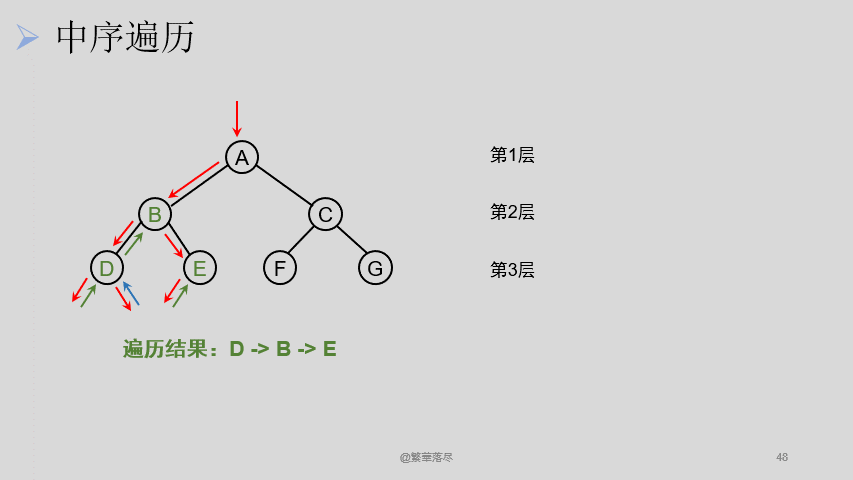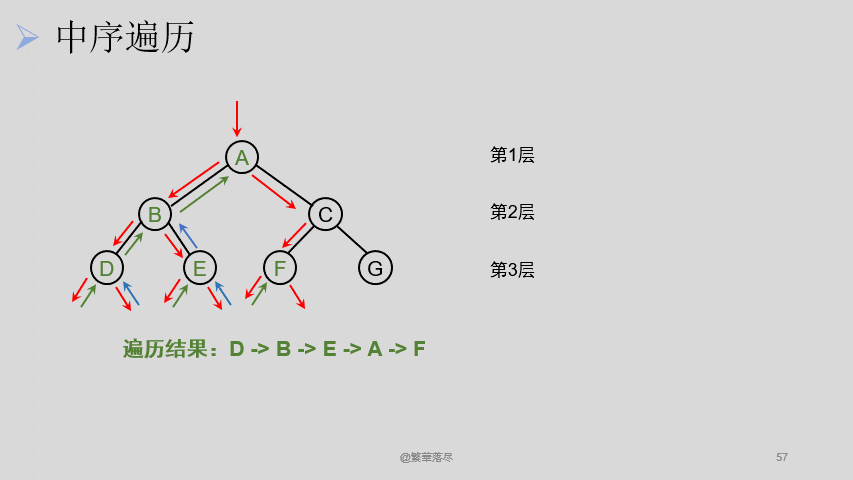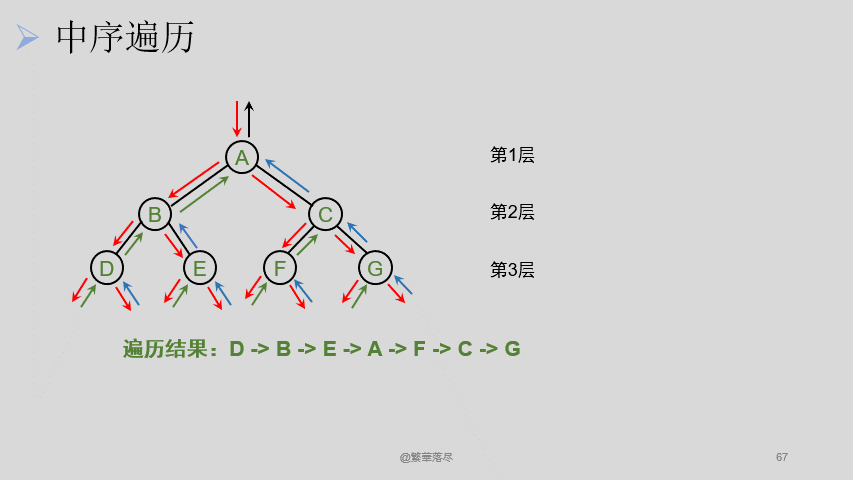
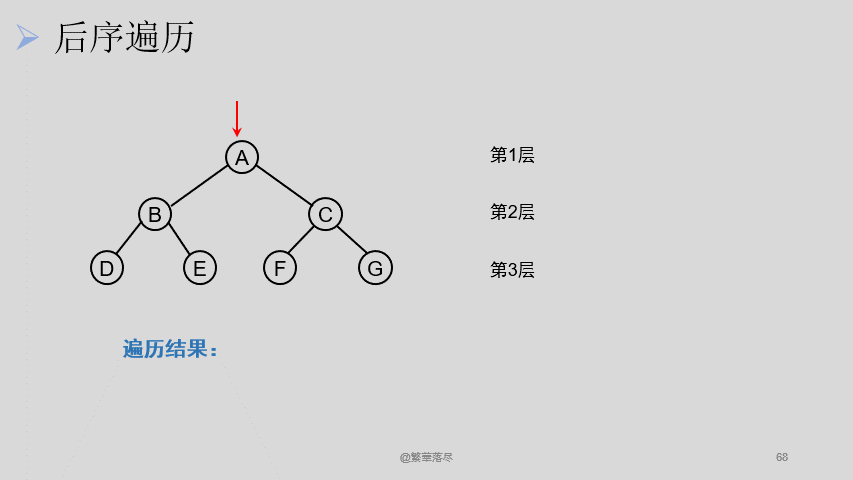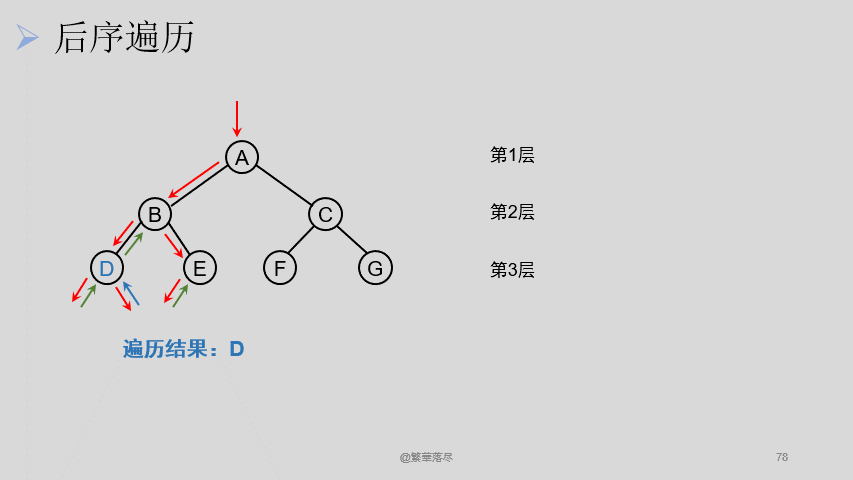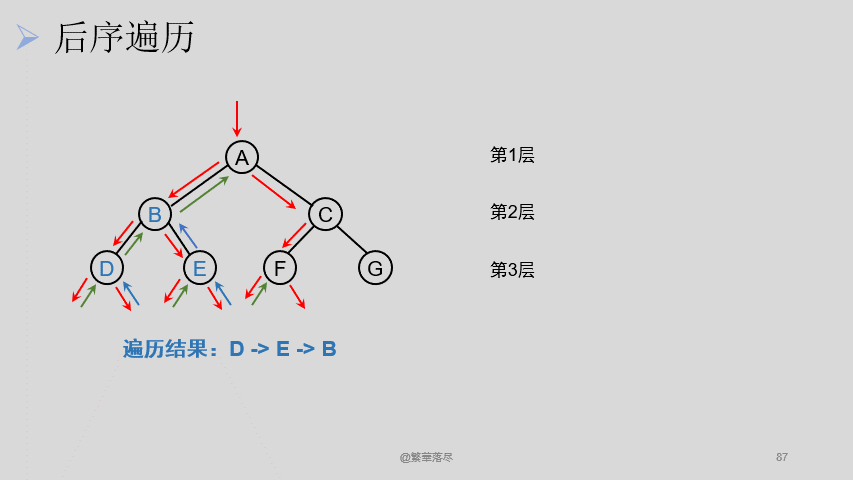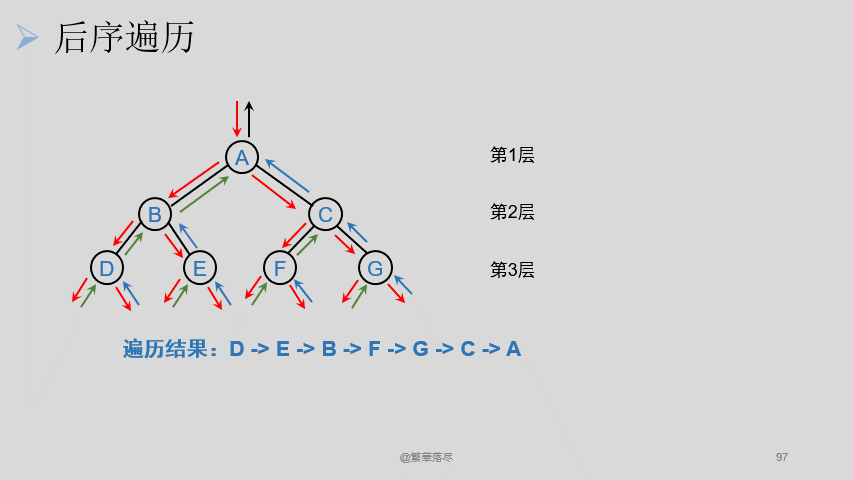
5.5后序遍历
后序遍历过程如下图所示: