LV03-12-数据结构-二叉树的遍历

发表于 分类于 ， ， 本文字数： 2.1k 阅读时长 ≈ 8 分钟

本文主要是数据结构——二叉树遍历实现的相关笔记，若笔记中有错误或者不合适的地方，欢迎批评指正😃。

点击查看使用工具及版本
Windows windows11
Ubuntu Ubuntu16.04的64位版本
VMware® Workstation 16 Pro 16.2.3 build-19376536
SecureCRT Version 8.7.2 (x64 build 2214) - 正式版-2020年5月14日
开发板 正点原子 i.MX6ULL Linux阿尔法开发板
uboot NXP官方提供的uboot，NXP提供的版本为uboot-imx-rel_imx_4.1.15_2.1.0_ga(使用的uboot版本为U-Boot 2016.03)
linux内核 linux-4.15(NXP官方提供)
STM32开发板 正点原子战舰V3(STM32F103ZET6)
点击查看本文参考资料
参考方向 参考原文
------
点击查看相关文件下载
数据结构 树 (密码:dmio)

1.树的结构体

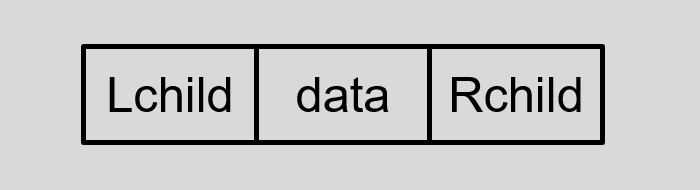
由前边的分析,存储结点需要两个指针域和一个数据域，如下图：

image-20220503060021813 
1
2
3
4
5
6
7
8
typedef char bitree_data; /* 定义二叉树中数据元素的数据类型 */

typedef struct bitree_node 
{
	bitree_data data;/* 数据域 */
	struct bitree_node *left; /* 指向左孩 */
	struct bitree_node *right;/* 指向右孩 */
}binarytree;/* binary tree node */

2.树的创建

要进行树的遍历，首先要有棵树吧，可是怎么去创建树，就直接一个一个结点在程序实现吗？如果结点比较多的话，那样得来的程序有点难以想象，并且也无法修改了。

前边学习树的基本概念的时候，可以知道，树可以理解为是由根结点和若干子树构成的，也就是说，树中还是树，其实这便形成了一种递归的数据结构，于是我们可以考虑使用递归函数来创建树。

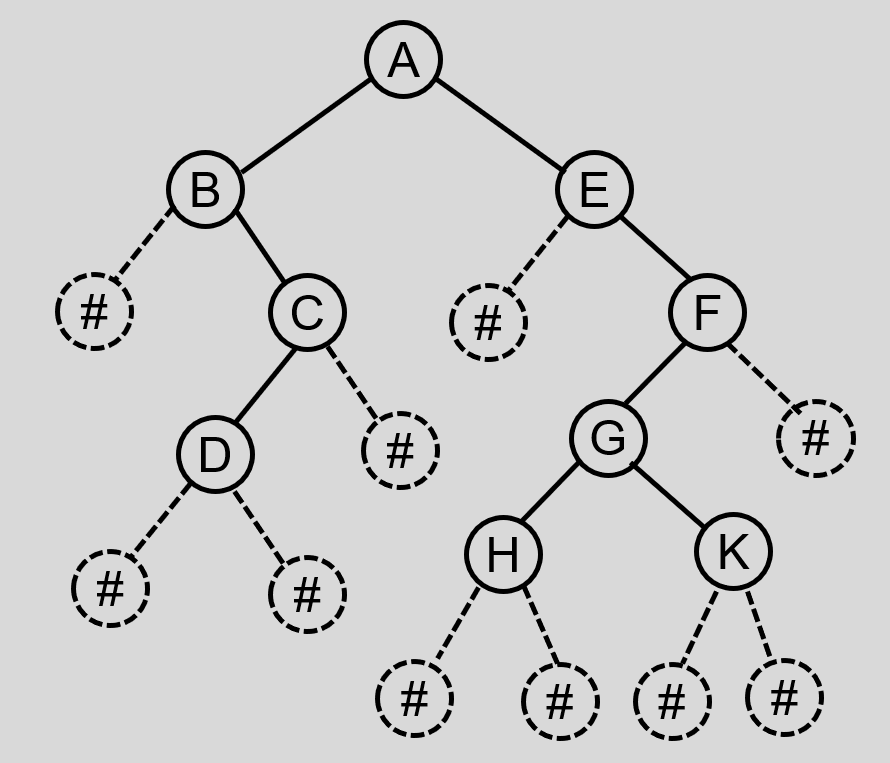
递归函数需要有结束的条件，我们可以规定输入#代表空，同时也是递归结束的条件。这个时候我们需要将待输入的二叉树补充成满二叉树，并且若有叶子结点，则也需要为叶子结点补充两个#孩结点以表示结束。如下图所示：

image-20220503062224535

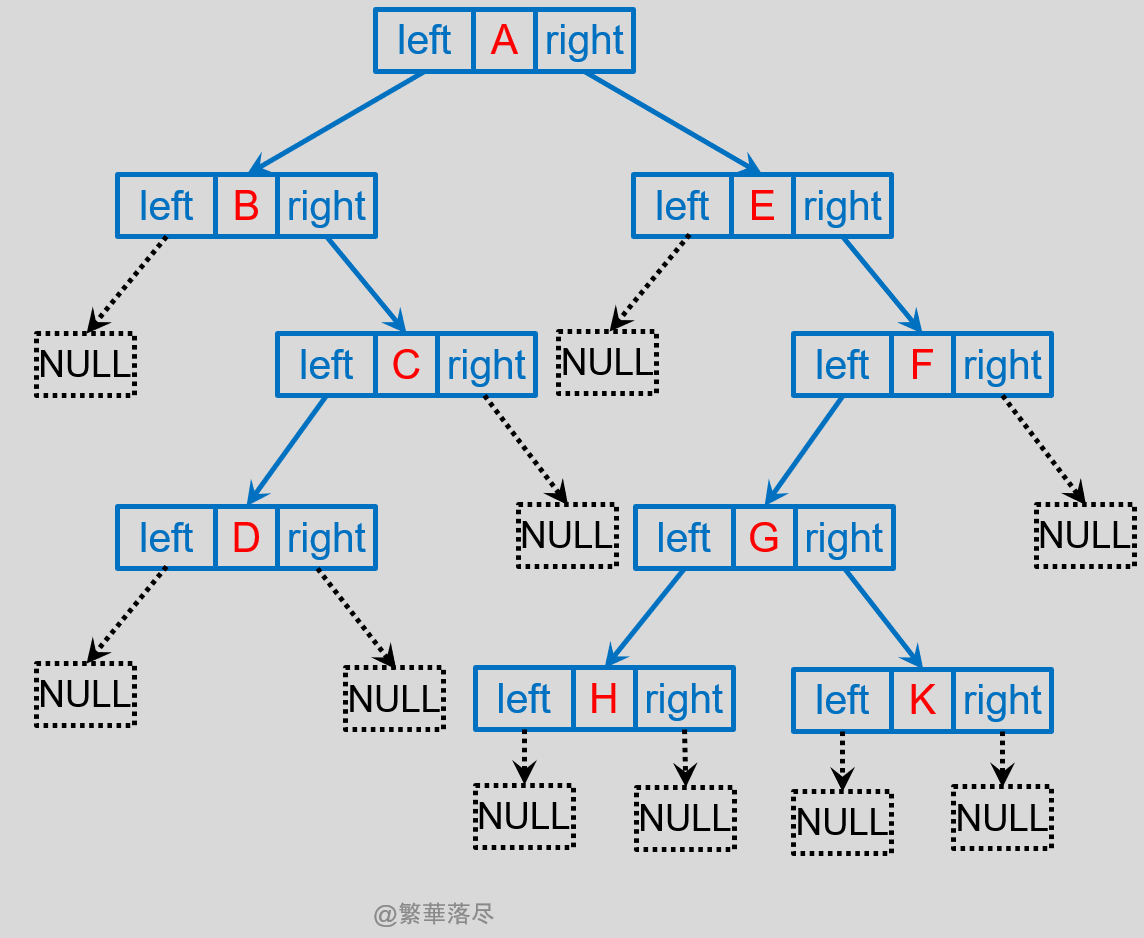
创建的链式存储结构如下图所示：

image-20220503062250922

于是，得到我们在输入的时候需要输入的序列为：

1
AB#CD###E#FGH##K###<Enter>

【注意】在递归函数的结束条件中尽量不要打印提示信息，不然每一次达到递归结束条件时都会打印相关提示，看起来还是比较乱的。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * @Function: binarytree_create
 * @Description: 二叉树创建
 * @param   : none
 * @return  : 返回一个地址
 *            NULL,创建失败;
 *            other,创建成功
 */
binarytree * binarytree_create()
{
	/* 定义一个接收输入的变量和一颗树的结构体指针变量 */
	bitree_data ch;
	binarytree * T;
	
	/* 1. 输入结点数据 */
	/* 不要在这里打印提示信息，否则每次递归到最后一层的时候都会打印一遍 */
	// printf("Please enter a data(# means enpty):");
	scanf("%c", &ch);
	if(ch == '#') /* 递归的返回条件 */
		return NULL;
	/* 2. 申请内存空间 */
	T = (binarytree *)malloc(sizeof(binarytree));
	/* 3. 判断是否申请成功 */
	if(T == NULL)
	{
		printf("binary tree malloc failed!\n");
		return NULL;
	}
	/* 4. 递归创建左右子树 */
	T->data = ch;
	T->left = binarytree_create();
	T->right = binarytree_create();
	
	return T;
}

3.先序遍历

【算法简述】：若二叉树为空树，则空操作；否则访问根结点，然后先序遍历左子树，最后先序遍历右子树。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @Function: preorder_traverse_recursive
 * @Description: 递归法先序遍历二叉树
 * @param T : 要遍历的二叉树树的地址
 * @return  : none
 */
void preorder_traverse_recursive(binarytree * T)
{
	/* 1. 判断树是否存在 */
	if(T == NULL)
	{
		/* 不要在这里打印提示信息，否则每次递归到最后一层的时候都会打印一遍 */
		// printf("\nbinary tree is not existed!\n");
		return;
	}
	/* 2. 访问结点数据 */
	printf("%c ", T->data);
	/* 3. 递归访问左右子树 */
	preorder_traverse_recursive(T->left);
	preorder_traverse_recursive(T->right);

}

4.中序遍历

【算法简述】：若二叉树为空树，则空操作；否则先中序遍历左子树，再访问根结点，最后中序遍历右子树。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * @Function: inorder_traverse_recursive
 * @Description: 递归法中序遍历二叉树
 * @param T : 要遍历的二叉树树的地址
 * @return  : none
 */
void inorder_traverse_recursive(binarytree * T)
{
	/* 1. 判断树是否存在 */
	if(T == NULL)
	{
		/* 不要在这里打印提示信息，否则每次递归到最后一层的时候都会打印一遍 */
		// printf("\nbinary tree is not existed!\n");
		return;
	}
	/* 2. 递归访问左右子树 */
	inorder_traverse_recursive(T->left);
	printf("%c ", T->data);
	inorder_traverse_recursive(T->right);

}

5.后序遍历

【算法简述】：若二叉树为空树，则空操作；否则先后序遍历左子树，然后后序遍历右子树，最后访问根结点。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * @Function: postorder_traverse_recursive
 * @Description: 递归法后序遍历二叉树
 * @param T : 要遍历的二叉树树的地址
 * @return  : none
 */
void postorder_traverse_recursive(binarytree * T)
{
	/* 1. 判断树是否存在 */
	if(T == NULL)
	{
		/* 不要在这里打印提示信息，否则每次递归到最后一层的时候都会打印一遍 */
		// printf("\nbinary tree is not existed!\n");
		return;
	}

	/* 2. 递归访问左子树 */
	postorder_traverse_recursive(T->left);
	/* 3. 递归访问右子树 */
	postorder_traverse_recursive(T->right);
	/* 4. 打印子树的根节点数据 */
	printf("%c ", T->data);

}

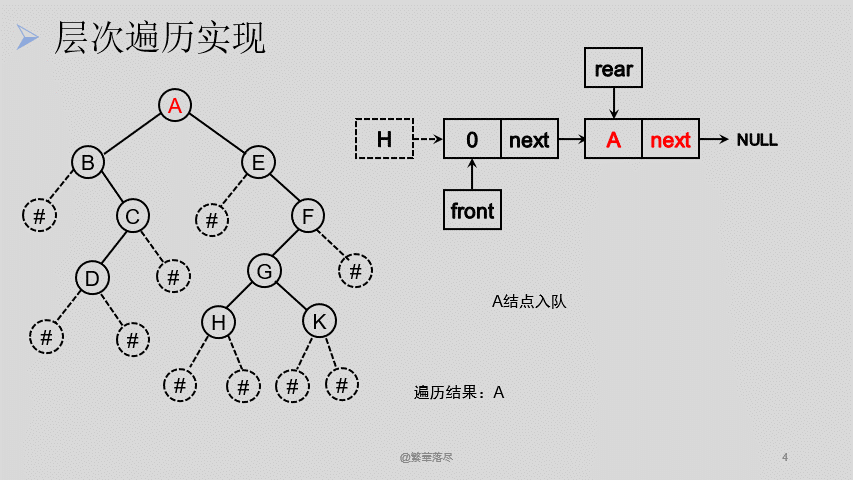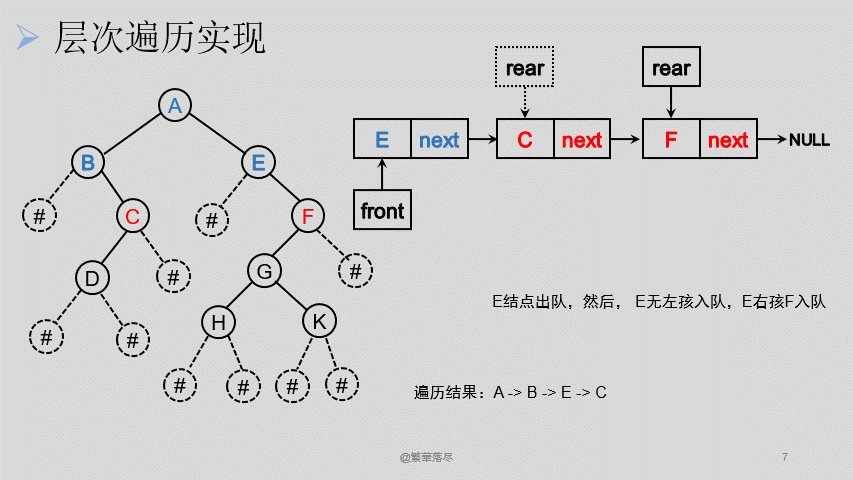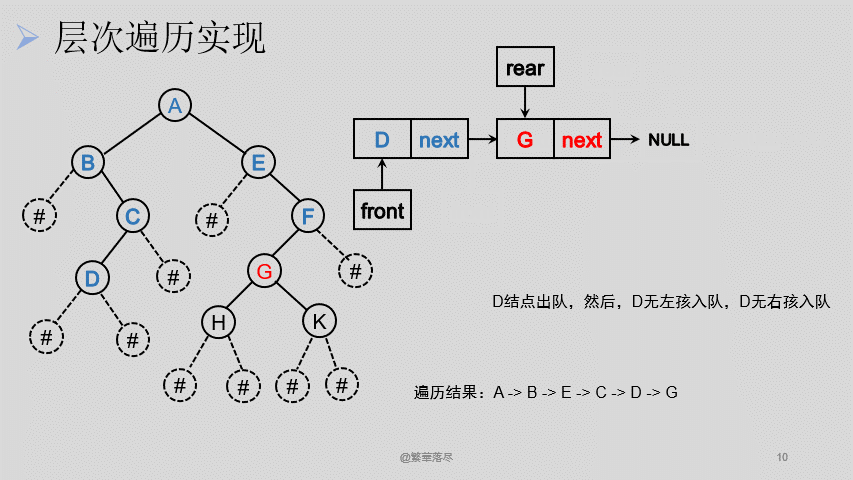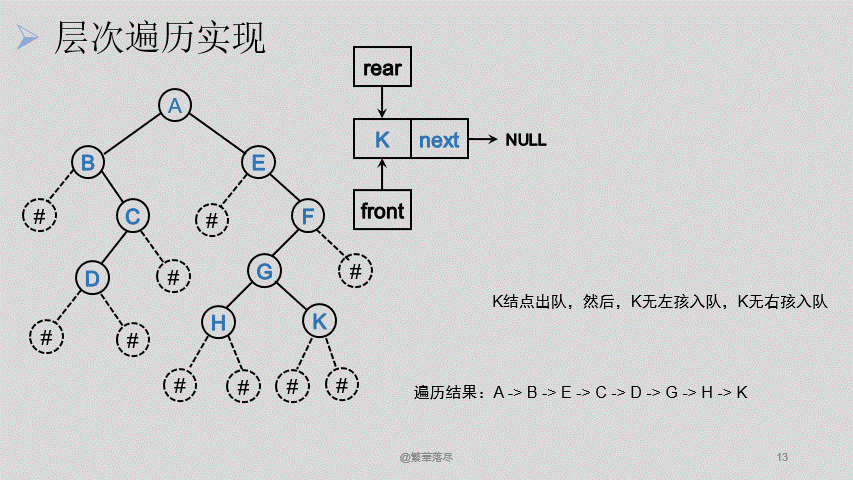
6.层次遍历

层次遍历借助链式队列实现，这里直接使用之前的链式队列实现文件，但是需要修改链式队列中存放的数据类型，以及一些相关函数中printf打印语句。

1
点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * @Function: layertorder_traverse_slinkedqueue
 * @Description: 链式队列实现层次遍历二叉树
 * @param T : 要遍历的二叉树树的地址
 * @return  : none
 */
void layertorder_traverse_slinkedqueue(binarytree * T)
{
	/* 定义一个链式队列结构体指针变量 */
	slqueue_lq * lq;
	/* 1. 创建链式队列 */
	if ((lq = slqueue_create()) == NULL) 
		return;
	/* 2. 判断树是否存在 */
	if(T == NULL)
	{
		printf("binary tree is not existed!\n");
		return;
	}
	/* 3. 打印根结点数据同时根结点入队 */
	printf("%c ", T->data);
	slqueue_enqueue(lq, T);
	while(!slqueue_empty(lq))
	{
		T = slqueue_dequeue(lq);
		if(T->left != NULL)
		{
			printf("%c ", T->left->data);
			slqueue_enqueue(lq, T->left);
		}
		if(T->right != NULL)
		{
			printf("%c ", T->right->data);
			slqueue_enqueue(lq, T->right);
		}
	}
	puts("");
	slqueue_free(lq);
}