LV03-13-数据结构-查找方法

发表于 分类于 ， ， 本文字数： 7.2k 阅读时长 ≈ 26 分钟

本文主要是数据结构——常见的查找方法相关笔记，若笔记中有错误或者不合适的地方，欢迎批评指正😃。

点击查看使用工具及版本
Windows windows11
Ubuntu Ubuntu16.04的64位版本
VMware® Workstation 16 Pro 16.2.3 build-19376536
SecureCRT Version 8.7.2 (x64 build 2214) - 正式版-2020年5月14日
开发板 正点原子 i.MX6ULL Linux阿尔法开发板
uboot NXP官方提供的uboot，NXP提供的版本为uboot-imx-rel_imx_4.1.15_2.1.0_ga(使用的uboot版本为U-Boot 2016.03)
linux内核 linux-4.15(NXP官方提供)
STM32开发板 正点原子战舰V3(STM32F103ZET6)
点击查看本文参考资料
参考方向 参考原文
------
点击查看相关文件下载
--- ---

1.查找

设记录表$L=(R_1,R_2,……,R_n)$，其中$R_i(l ≤ i ≤n)$为记录，对给定的某个值 k ，在表 L 中确定 key = k 的记录的过程，称为查找。若表 L 中存在一个记录$R_i$的 key = k ，记为$R_i.key = k$，则查找成功，返回该记录在表L中的序号 i (或$R_i $的地址)，否则(查找失败)返回 0 (或空地址 NULL )。表 L 就称为查找表，它是是由同一类型的数据元素构成的集合。

在查找表中只做查找操作，而不改动表中数据元素，称此类查找表为静态查找表，静态查找表既可以使用顺序表表示，也可以使用链表结构表示。反之，在查找表中做查找操作的同时进行插入数据或者删除数据的操作，称此类表为动态查找表。

查找的方法有这几种：顺序查找，二分查找（折半查找），分块查找和 hash 表查找等。

  • 平均查找长度

对查找算法，主要分析其 T(n) （时间复杂度）。查找过程是 key 的比较过程，时间主要耗费在各记录的 key 与给定 k 值的比较上。比较次数越多，算法效率越差（即 T(n) 量级越高），故用比较次数刻画算法的 T(n) 。

平均查找长度 ASL （ Average Search Length ）：对给定 k ，有 n 个元素的查找表 L 中记录比较次数的期望值(或平均值)，即
$$
ASL=\sum_{i = 1}^{n}P_iC_i
$$
$P_i$为查找$R_i$的概率。等概率情况下$P_i=1/n$；$C_i$为查找$R_i$时$key$进行的比较次数(或查找次数)。

2.顺序查找

2.1查找方法

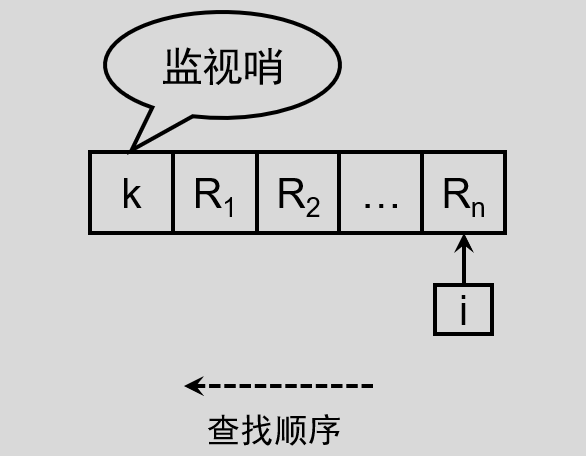
静态查找表用顺序存储结构表示时，顺序查找的查找过程为：设给定值为 k ，在表$L=(R_1,R_2,……,R_n)$中，从$R_n$开始，查找$key = k$的记录。

实现代码如下：

1
2
3
4
5
6
7
8
9
int sqsearch(seqlist r, keytype k)  
{   
    int i;
	r.data[0].key = k;  /* k存入监视哨 */
	i = r.len;          /* 取表长 */
	while(r.data[i].key != k) 
        i--;  
	return (i);
}
点击查看什么是监视哨

在程序中初始化创建查找表时，由于是顺序存储，所以会将所有的数据元素存储在数组中，但是把第一个位置留给了用户用于查找的关键字，顺序表的一端添加用户用于搜索的关键字，称作监视哨。

image-20220503144415215

2. ASL

表中有 n 个数据元素，查找第一个元素时需要比较 n 次；查找最后一个元素时需要比较 1 次，所以有 $C_i = n – i + 1$，假设这 n 个数的被查找到的概率是相同的，则有：
$$
ASL = \sum_{i = 1}^n\frac{1}{n}(n - i + 1) = \frac{n+1}{2}
$$
这个平均查找长度是在假设查找算法每次都成功的前提下得出的。而对于查找算法来说，查找成功和查找失败的概率是相同的，查找算法的平均查找长度应该为查找成功时的平均查找长度加上查找失败时的平均查找长度。若每次都查找失败，那么比较的次数都是 n + 1 ，所以最终 ASL 为：
$$
ASL = \frac{1}{2}\sum_{i = 1}^n\frac{1}{n}(n - i + 1) + \frac{1}{2}(n + 1) = \frac{3}{4}(n + 1)
$$
【缺点】这样算下来，查找的效率是很低的，查找某记录几乎要扫描整个表，当表长 n 很大时，会令人无法忍受。

3.二分查找

3.1查找方法

二分查找也叫作折半查找，在某些情况下相比于顺序查找，效率会更高。但是该算法的使用的前提是静态查找表中的数据必须是有序的。

算法思路：对给定值 k ，逐步确定待查记录所在区间，每次将搜索空间减少一半(折半)，直到查找成功或失败为止。

设两个游标 low 、 high ，分别指向当前待查找表的上界(表头)和下界(表尾)， mid 指向中间元素。

点击查看中间元素计算

$$
mid = [\frac{low + high}{2}]
$$
很多时候， mid 计算出来并不为整数，所以还需要进行取整操作。

如下图所示：

1

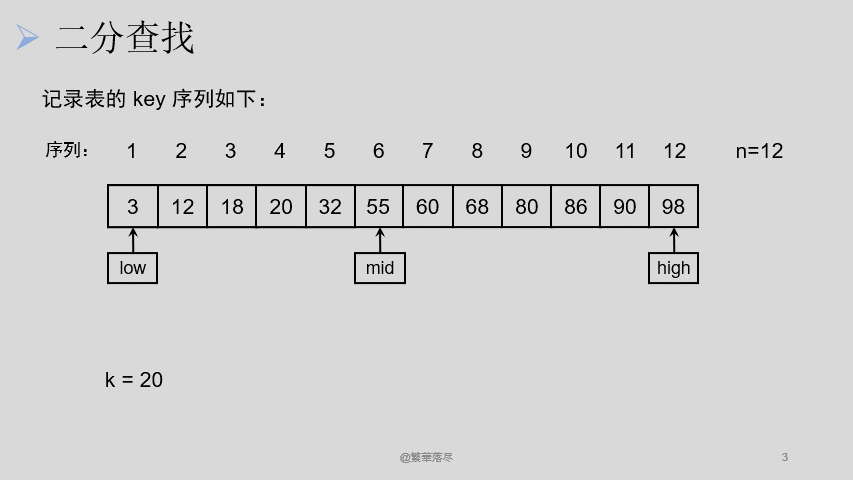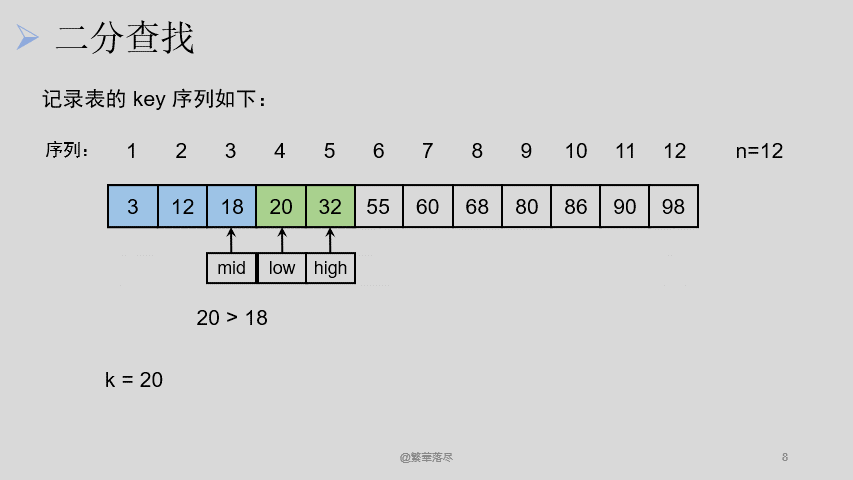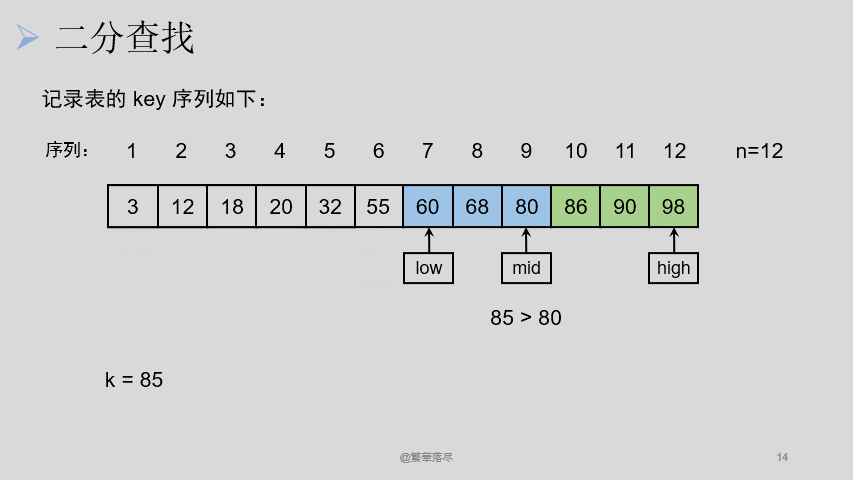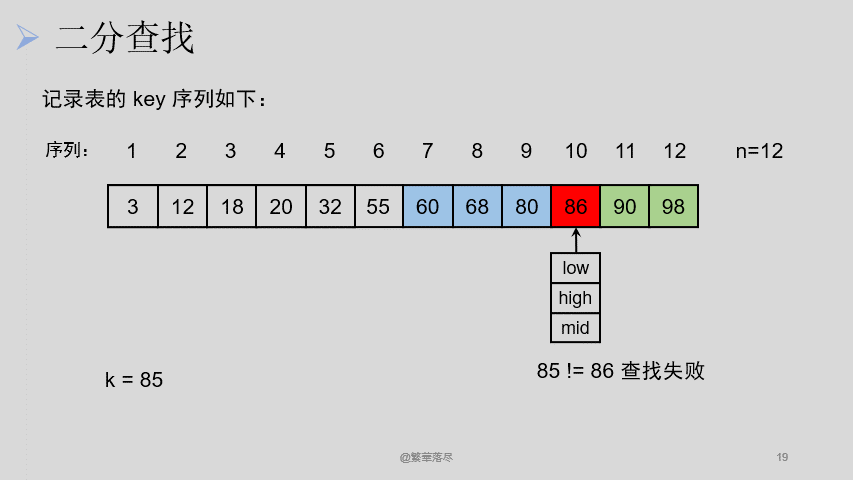
实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int Binsearch(seqlist r, keytype k)    /* 对有序表 r 折半查找的算法 */
{  
    int low, high, mid;  
    low = 1;
	high = r.len; 
    while (low <= high)    
    {  
        mid = (low+high) / 2;   
        if (k == r.data[mid].key)  
            return (mid);  
        if (k < r.data[mid].key) 
            high = mid - 1;  
        else 
            low = mid + 1;
    }      
     return 0;
 }

3.2 ASL

折半查找的运行过程可以用二叉树来描述，这棵树通常称为判定树。把当前查找区间的中间位置上的结点作为根，左子表和右子表中的结点分别作为根的左子树和右子树，由此得到的二叉树，称为描述二分查找的判定树( Decision Tree )或比较树。

二叉判定树怎么画？
  • 长度为 n 的查找表二叉判定树构造方法：

（1）当 n = 0 时，二分查找判定树为空；

（2）当 n ＞ 0 时，二分查找判定树的根结点是查找表中序号为 mid = (1 + n) / 2 的记录，根结点的左子树是与有序表 L[1] ~ L[mid - 1] 相对应的折半查找判定树，根结点的右子树是与 L[mid + 1] ~ L[n] 相对应的二分查找判定树。

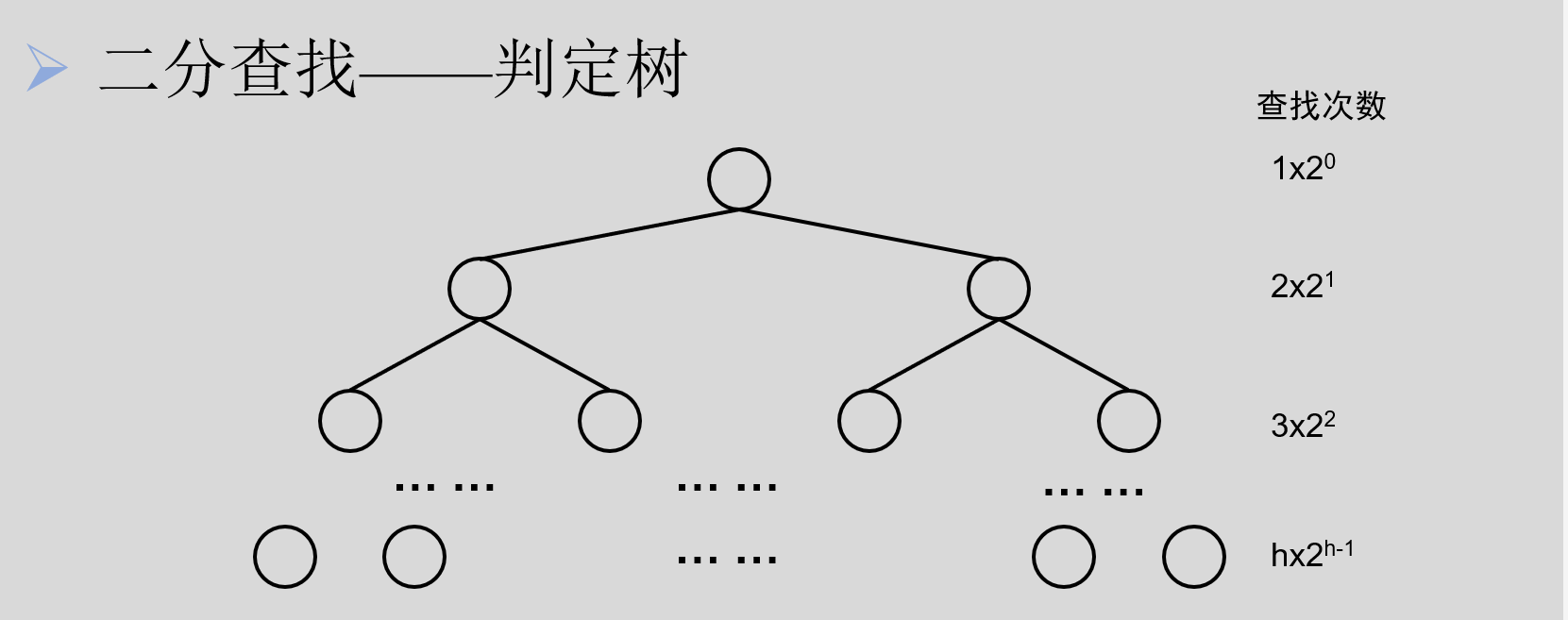
image-20220503181717869

假设表长$n = 2^h -1$，$h = \log_2(n+1)$，记录数 n 恰好为一棵 h 层的满二叉树的结点数，则得出的判定树如上图。此时有：
$$
ASL = \sum_{i=1}^nP_iC_i=\frac{1}{n}\sum_{i=1}^hi·2^{i-1}
$$

$$
\text{令} S = \sum_{i=1}^hi·2^{i-1}=1·2^0+2·2^1+3·2^2+…+(h-2)·2^{h-2}+(h-1)·2^{h-1}
$$

$$
\text{则} 2S = 2·\sum_{i=1}^hi·2^{i-1}=1·2^1+2·2^2+3·2^3+…+(h-2)·2^{h-1}+(h-1)·2^{h}
$$

$$
\text{则} S = 2S - S = h·2^{h}-(2^0+2^1+2^2+…+2^{h-2}+2^{h-1})=h·2^h-(2^h-1)=(n+1)\log_2(n+1)-n
$$

$$
\text{所以} ASL=\frac{n+1}{n}\log_2(n+1)-1
$$

二分查找法的平均查找长度显然要比顺序查找方法更优。

4.分块查找

4.1查找方法

分块查找，也叫索引顺序查找，算法实现除了需要查找表本身之外，还需要根据查找表建立一个索引表。

  • 分块

设记录表长为 n ，将表的 n 个记录分成$b=[n/s]$个块，每块 s 个记录（最后一块记录数可以少于 s 个），即：

image-20220503190730938

且表分块有序，即第 i（1 ≤ i ≤ b-1） 块所有记录的 key 小于第 i + 1 块中记录的 key ，但块内记录可以无序。

  • 建立索引

每块对应一个索引项，其中$k_{max}$为该块内记录的最大 key ， link 为该块第一记录的序号（或指针）。

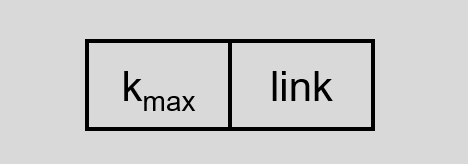
image-20220503191008660
点击查看实例

设表长为 n = 8 ，取 s = 3 ，$b = [8/3]=3$，即分为 3 块，每块 3 个元素，最后一块不足 3 个元素，只有两个元素。如下图所示：

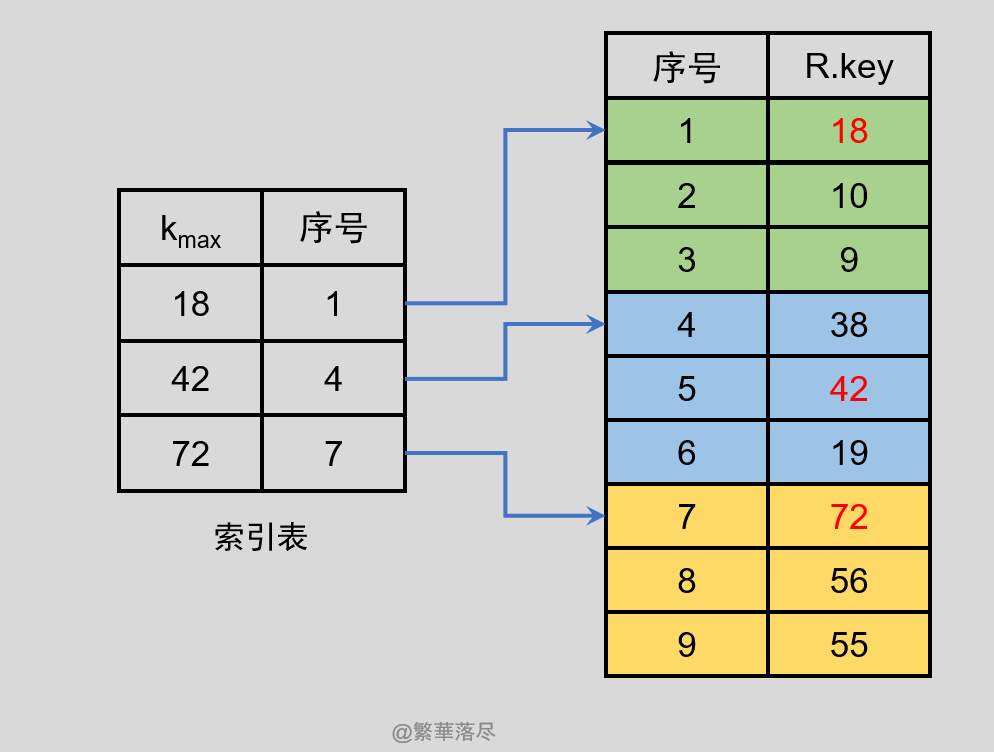
image-20220503192432254

若查找 k = 19 的记录，索引表是按照$k_{max}$有序的，可对其折半查找，而块内按顺序方法查找。

4.2 ASL

分块查找算法的运行效率受两部分影响：查找块的操作和块内查找的操作。查找块的操作可以采用顺序查找，也可以采用折半查找（会更好一些）。块内查找的操作采用顺序查找的方式。

相比于折半查找，分块查找时间效率上更低一些。相比于顺序查找，由于在子表中进行，比较的子表个数会不同程度的减少，所有分块查找算法会更优。

总的来说。分块查找的 ASL 介于顺序查找和二分查找之间。

5. Hash 表

上边介绍了三种查找方法，但是都是需要经过大量的比较。其实理想的查找方法是：对给定的 k ，不经任何比较便能获取所需的记录，其查找的时间复杂度为常数级 O(C) 。这就要求在建立记录表的时候，确定记录的 key 与其存储地址之间的关系 f ，即使 key 与记录的存放地址 H 相对应：

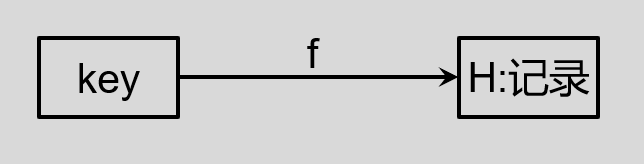
image-20220504064720751

当我们需要查找 key = k 的记录时，通过关系 f 就可得到相应记录的地址而获取记录，从而免去了 key 的比较过程，这个关系 f 就是所谓的 Hash 函数（或称散列函数、杂凑函数），记为 H(key) 。 H(key) 实际上是一个地址映象函数，其自变量为记录的 key ，函数值为记录的存储地址（或称 Hash 地址）。

不同的 key 可能得到同一个 Hash 地址，即当 keyl != key2 时，可能有 H(key1) = H(key2) ，此时称 key1 和 key2 为同义词。这种现象称为冲突或碰撞，因为一个数据单位只可存放一条记录。选取 Hash 函数只能做到使冲突尽可能少，却不能完全避免。

根据选取的 Hash 函数 H(key) 和处理冲突的方法，将一组记录$(R_1 R_2……R_n)$映象到记录的存储空间，所得到的记录表称为 Hash 表。

image-20220504065758723

5.1 Hash 函数构建

在设计哈希函数时，要尽量地避免冲突现象的发生。常用的 Hash 函数构造方法有这几种：直接定址法、数字分析法、平方取中法、折叠法、随机数法和除留余数法。

5.1.1直接定址法

直接定址法的 Hash 函数是一次函数：
$$
H(key) = a * key + b
$$
其中 H（key） 表示关键字为 key 对应的哈希地址， a 和 b 都为常数。

例如，很多时候我们接受了服务后，都可能会对客服做评价，评价分数为 60 、 70 、 80 、 90 、 100 这几个层次，通过直接定址法建立 Hash 表：

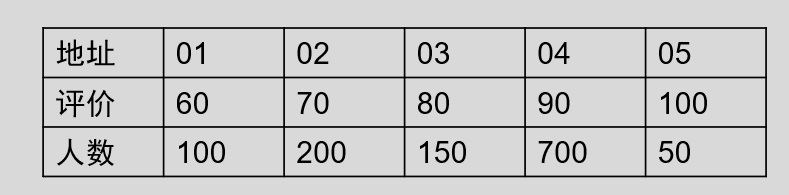
image-20220504071459246

现在我们要查找 90 分的人数，那么我们带入 90 到 Hash 中，会直接得到其 Hash 地址 04 （求得的哈希地址表示该记录的位置在查找表的第 04 位）。

5.1.2数字分析法

如果关键字由多位字符或者数字组成，就可以考虑抽取其中的 2 位或者多位作为该关键字对应的哈希地址，在取法上尽量选择变化较多的位，避免冲突发生。

例如，下图为一组数据的部分关键字，他们都是由 10 位十进制数（全为 0-9 ）组成的:

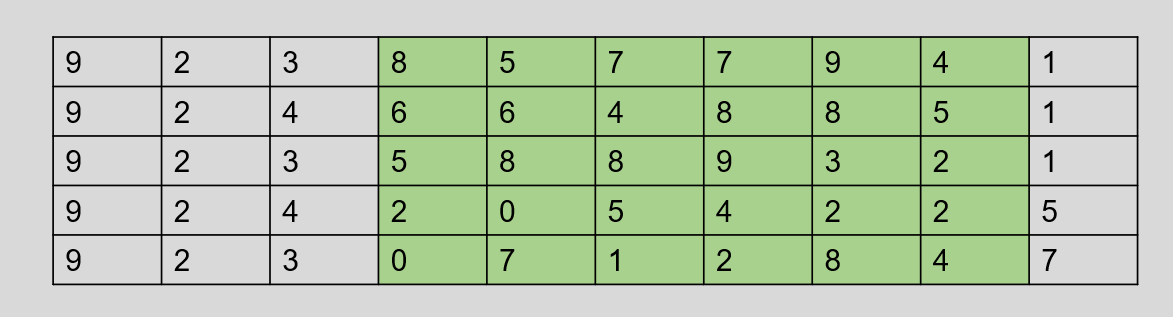
image-20220504072213357

通过分析关键字的构成，很明显可以看到只有中间绿色部分取值近似随机，所以为了避免冲突，可以这一部分中任意选取 几 位作为其哈希地址。

5.1.3平方取中法

平方取中法就是对关键字做平方操作，取中间得几位作为哈希地址。例如，

image-20220504075444324

可以看到平方后开头两位各不相同，于是可以取开头两位作为其 Hash 地址。

5.1.4折叠法

折叠法是将关键字分割成位数相同的几部分（最后一部分的位数可以不同），然后取这几部分的叠加和（舍去进位）作为哈希地址。折叠的方式有两种，一种是移位折叠，一种是间界折叠。

例如，图书馆某本书的编号为 0-520-1314-5 ，则有：

image-20220504080829381

移位折叠就是将分割后的每一小部分，按照其最低位进行对齐，然后相加；间界折叠是从一端向另一端沿分割线来回折叠。

5.1.5随机数法

随机数法就是取关键字的一个随机函数值作为它的 Hash 地址，即： H(key)=random（key） ，此方法适用于关键字长度不等的情况。这里的随机函数其实是伪随机函数，随机函数是即使每次给定的 key 相同，但是 H(key) 都是不同，而伪随机函数正好相反，每个 key 都对应的是固定的 H(key) 。

5.1.6除留余数法

若已知整个 Hash 表的最大长度 m ，可以取一个不大于 m 的数 p ，然后对该关键字 key 做取余运算，即： H(key) = key % p 。例如，

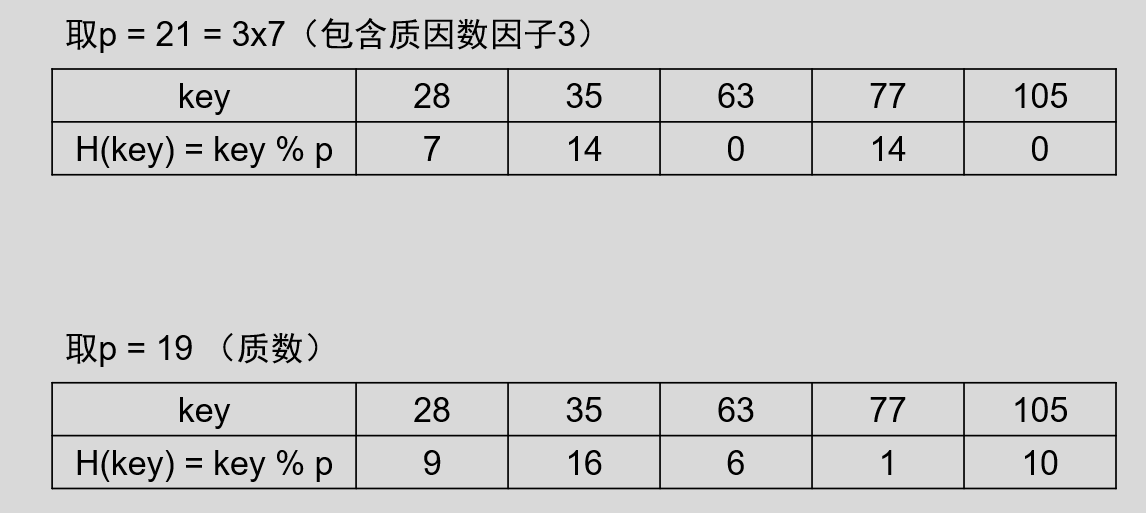
image-20220504082409289

由上图可知， p = 21 时，包含质数因子 7 的 key 都可能被映象到相同的单元，冲突现象严重。当 p = 19 时， H(key) 的随机度就好多了。

【注意】对于 p 的取值非常重要，一般来说 p 可以为不大于 m 的质数或者不包含小于 20 的质因数的合数。

5.2冲突处理

选取随机度好的 Hash 函数可使冲突减少，一般来讲不能完全避免冲突。设 Hash 表地址空间为 0～m-1 （表长为 m ）:

image-20220504103516463

表中某地址$j \in [0，m-1]$中己存放有记录，而另一个记录的 H(key) 值也为 j 此时就会产生冲突。

处理冲突的方法一般为：在地址 j 的前面或后面找一个空闲单元存放冲突的记录，或将相冲突的诸记录拉成链表。在处理冲突的过程中，可能发生一连串的冲突现象，即可能得到一个地址序列$H_1,H_2,…,H_n,H_i\in[0，m-1]$。$H_1$是冲突时选取的下一地址，而$H_1$中可能己有记录，又需要设法得到下一地址$H_2$，直到某个$H_n$不发生冲突为止。这种现象称为聚积，它严重影响了 Hash 表的查找效率，聚积的发生也会加重冲突。

还有一个重要的因素是表的装填因子 α ， α = n / m ，其中 m 为表长， n 为表中记录个数。一般 α 在 0.7～0.8 之间，使表保持一定的空闲余量，以减少冲突和聚积现象。

5.2.1开放地址法

当发生冲突时，在 H(key) 的前后找一个空闲单元来存放冲突的记录，即在 H(key) 的基础上获取下一地址：
$$
H_i = (H(key) + d_i)%m
$$
其中 m 为表长， % 运算是保证$H_i$落在 [0，m-1] 区间；$d_i$为地址增量，它的取法有多中种：

（1）线性探测法：$d_i = 1,2,3,…,(m-1)$，即当遇到冲突时，从发生冲突位置起，每次 +1 ，向右探测，直到有空闲的位置为止。

（2）二次探测法：$d_i = 1^2,-1^2,2^2,-2^2,…$，即从发生冲突的位置起，按照 如$+1^2,-1^2,+2^2,-2^2,…$此探测，直到有空闲的位置。

（3）伪随机数探测法：$d = \text{伪随机数}$，即每次加上一个随机数，直到探测到空闲位置结束。

  • 实例

设记录的 key 集合 k = {23, 34, 14, 38, 46, 16, 68, 15, 7, 31, 26} ，记录数 n = 11 ，令装填因子 α = 0.75 ，则表长 m = [n / α] = 15 ，使用除留余数法选取 Hash 函数，取 p = 13 ，则 H(key) = key % 13 ，建立 Hash 表，则有：

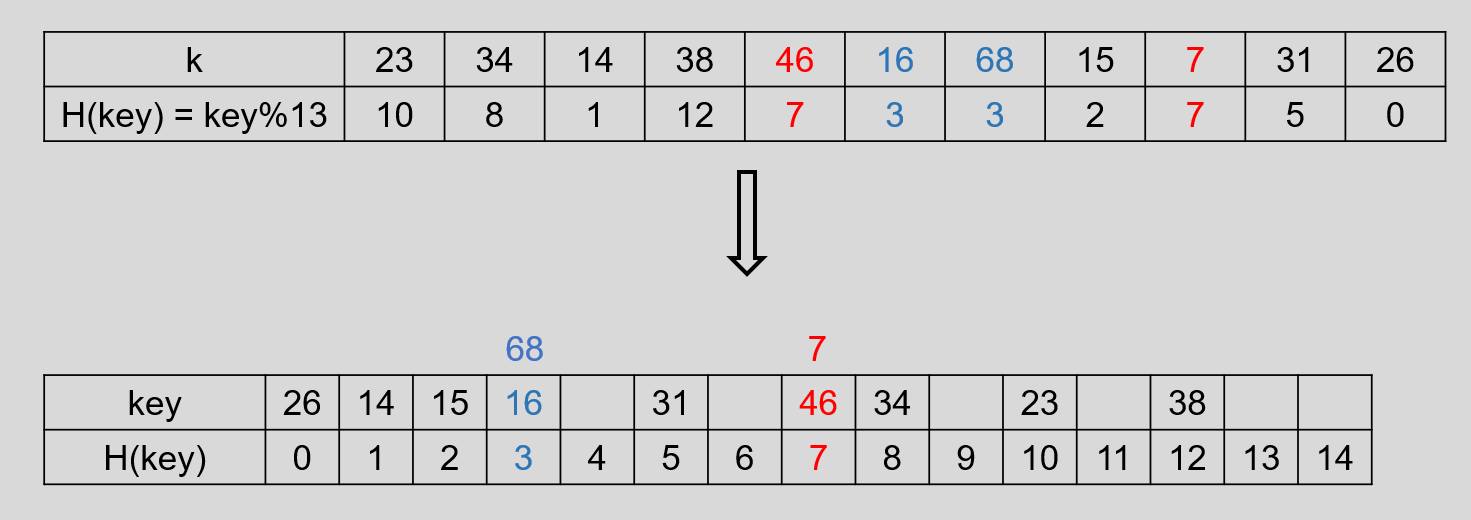
image-20220504110838954

会发现有两个地方产生了冲突，下边使用开放地址法进行处理，重新放置的地址为：
$$
H_i = (H(key)+d_i)%15
$$
所以有：

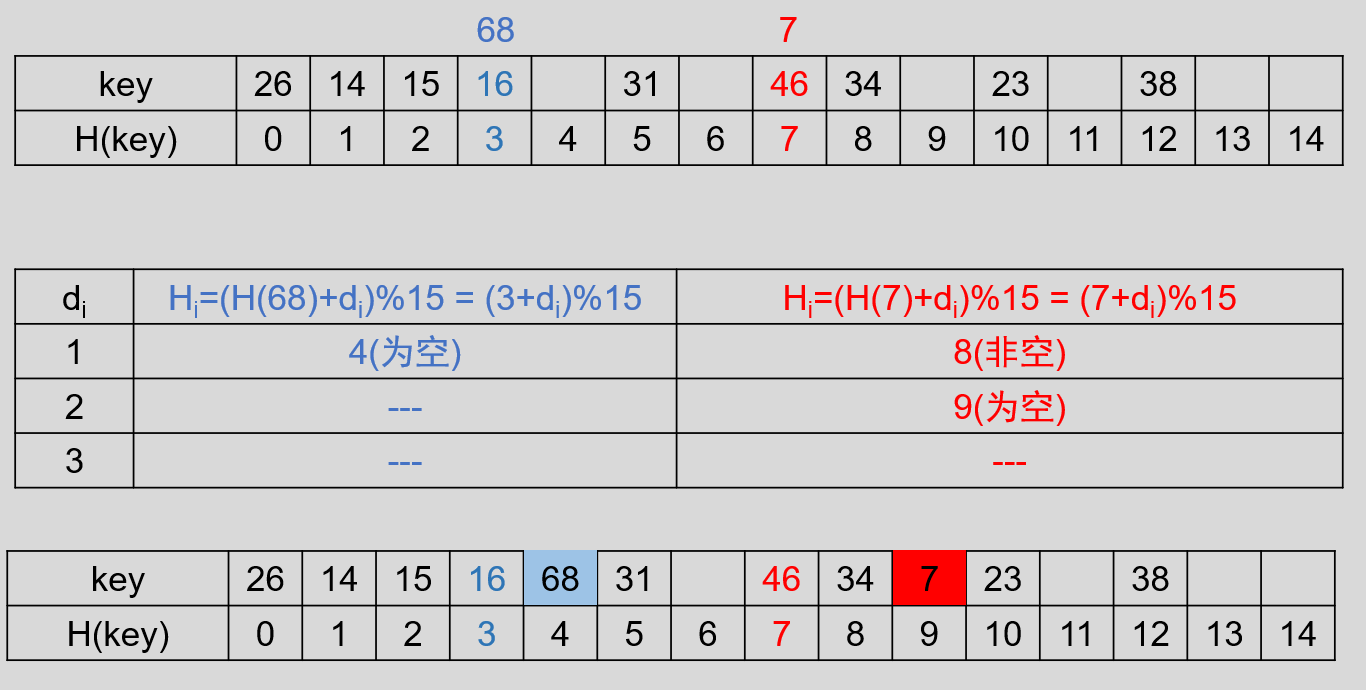
image-20220504112037009

5.2.2链地址法

我们还可以在发生冲突时，将各冲突记录链在一起，即同义词的记录存于同一链表。即可以设 H(key) 取值范围（值域）为 [0，m-1] ，建立头指针向量 HP[i] (0 ≤ i ≤ m-1) ，其中 HP[i] 初始值为空。

HP[i]（0≤i≤m-l）初值为空。

  • 实例

设记录的 key 集合 k = {23, 34, 14, 38, 46, 16, 68, 15, 7, 31, 26} ，则通过 Hash 函数 H(key) = key % 13 得到：

image-20220504112848906

通过链地址法建立 Hash 表，则有：

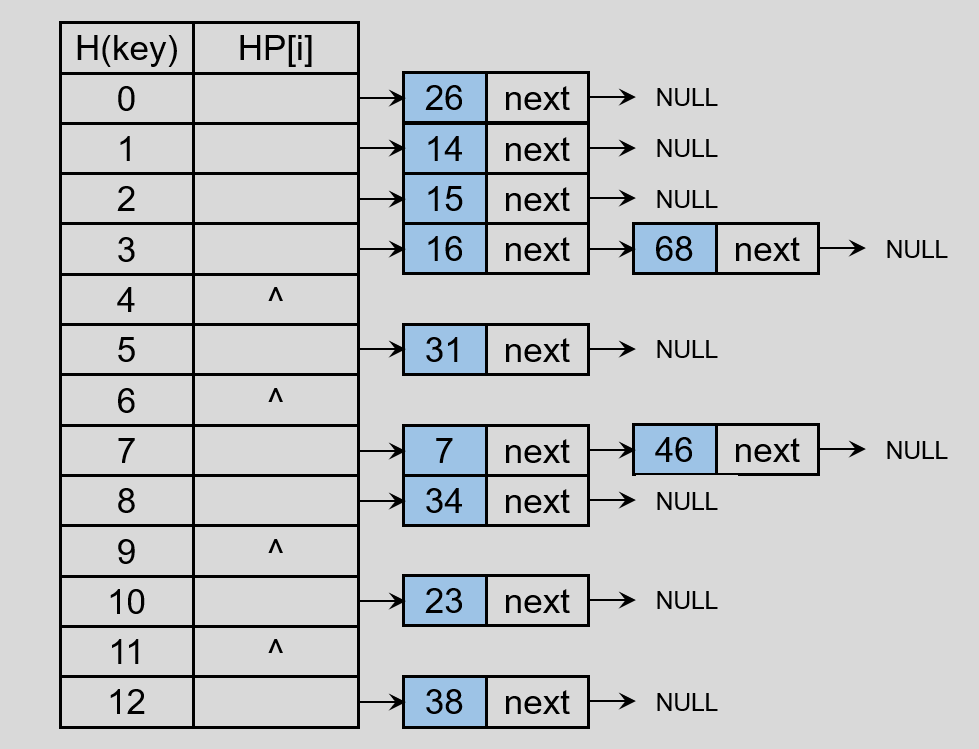
image-20220504114749785

链地址法解决冲突的优点：无聚积现象；删除表中记录容易实现。

5.3结构体实现

首先我们需要一个数组存储 Hash 表地址，这个其实是用于存储 key 对 p 取的余数，接着后边使用链地址法处理所有冲突，链表节点我们使用三个域表示，数据域 key 存储原始数据，数据域 value 存储余数，也就是数据在 Hash 表中的地址，最后是一个指针域，指向下一个节点。节点结构如下图：

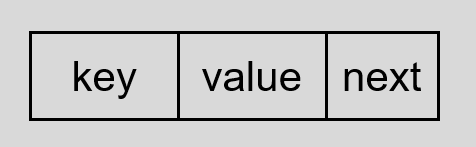
image-20220504153925233

结构体定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/* 宏定义 */
#define N 12 /* Hash表长度 */

/* 自定义数据类型 */
typedef int data_h;

typedef struct hash_node 
{
	data_h key;  /* 存放原始的数据 */
	data_h value;/* 存放余数 */
	struct hash_node * next;
}hslinkednode, * hslinkedlink;

typedef struct 
{
	hslinkednode data[N]; /* 地址表 */
}hash;

5.4 Hash 表基本操作

完整源代码可点击这里下载：

数据结构 查找 (密码:b1y3)

5.4.1创建

创建一个 Hash 表数组，数组中每个元素都是 Hash 表节点类型，如下图：

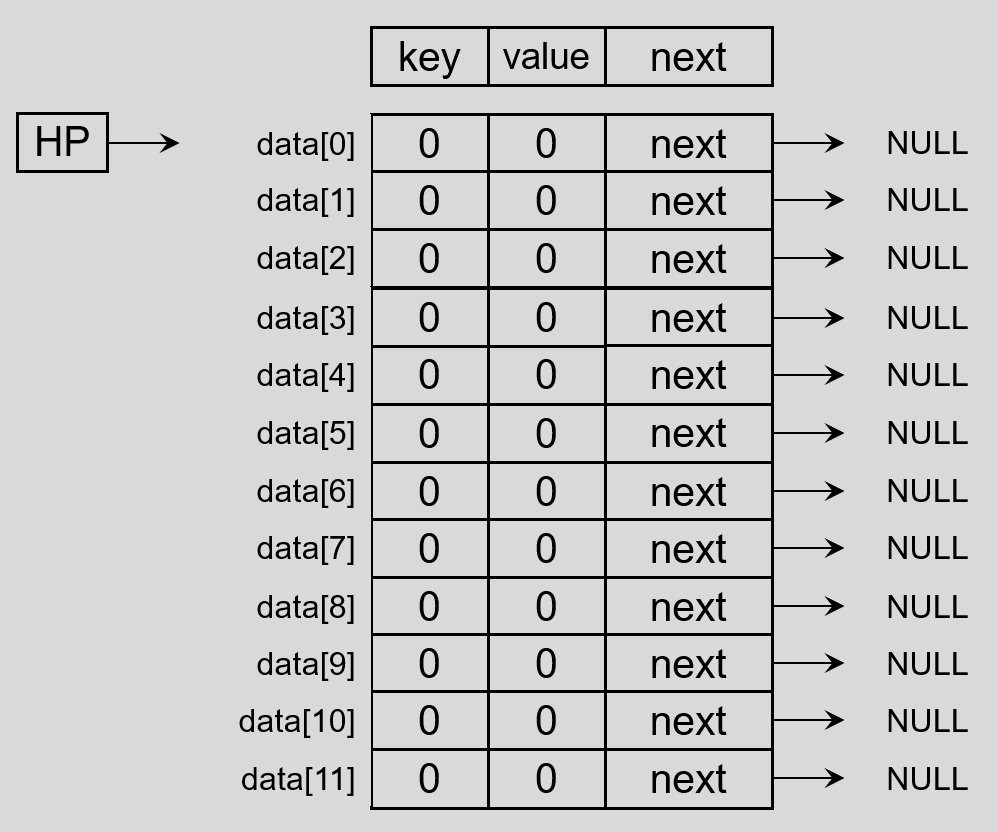
image-20220504163214158

【注意】数组中的元素，后边都相当于链表头节点。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * @Function: slinkedlist_create
 * @Description: Hash表创建
 * @param   : none
 * @return  : 返回一个地址
 *            NULL,内存申请失败;
 *            HP,Hash表地址
 *
 */
hash * hashlist_create()
{
	/* 定义一个Hash表结构体指针变量 */
	hash * HP;
	/* 1. 申请内存空间 */
	HP = (hash *)malloc(sizeof(hash));
	/* 2. 判断是否申请成功 */
	if (HP == NULL)
	{
		printf(" hash list malloc failed!\n");
		return HP;
	}
	/* 3. 初始化内存空间 */
	memset(HP, 0, sizeof(hash));

	return HP;
}

5.4.2插入

插入节点的过程如下图所示：

2

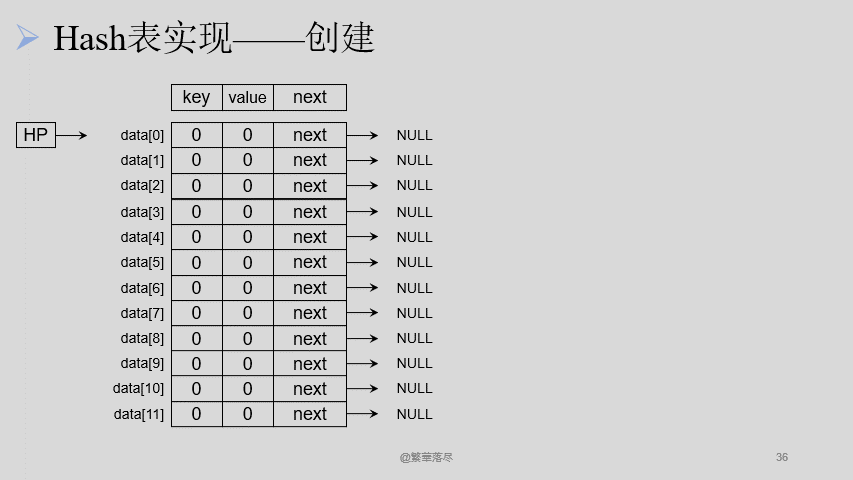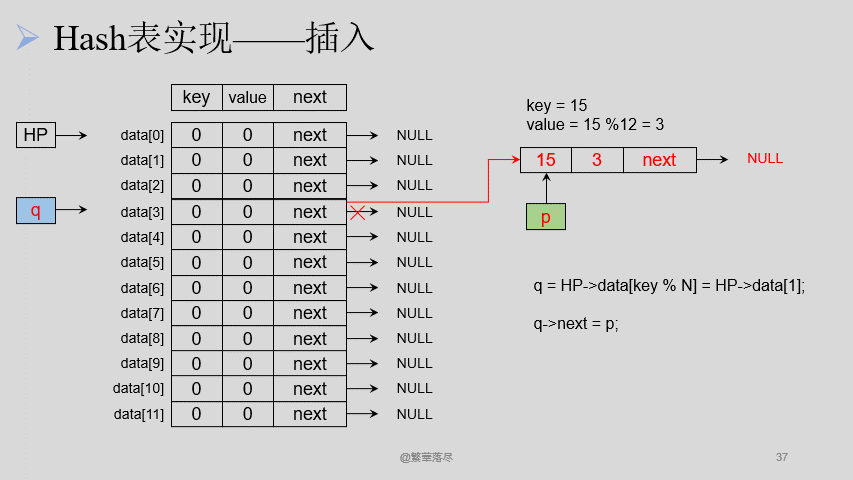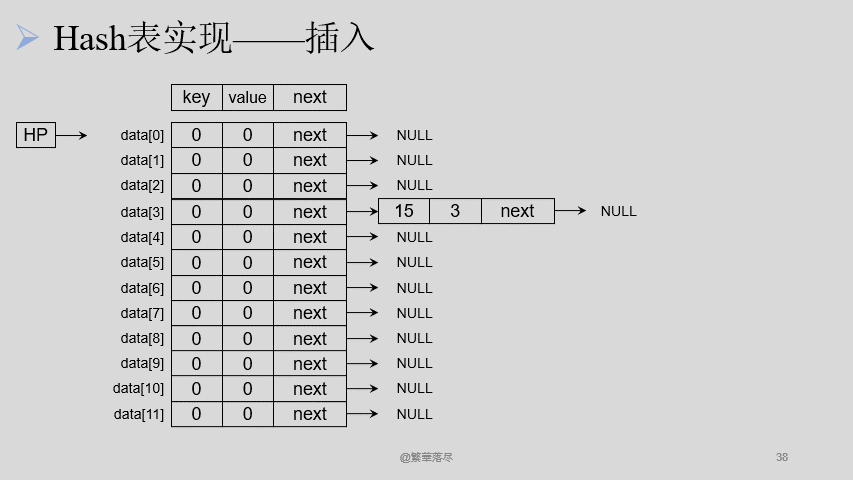
【注意】当产生冲突的时候，可以将数据通过链表相连接，在插入的时候注意有序插入。

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * @Function: hashlist_insert
 * @Description: Hash表数据插入
 * @param HP: Hash表地址
 * @param key: 要插入的数据
 * @return  : 返回一个数值
 *            0,插入成功;
 *            -1,Hash表不存在或者节点内存申请失败
 *
 */
int hashlist_insert(hash * HP, data_h key)
{
	/* 定义两个Hash表节点结构体指针变量 */
	hslinkedlink p;
	hslinkedlink q;
	/* 1. 判断Hash表是否存在 */
	if (HP == NULL)
	{
		printf(" hash list is not exited!\n");
		return -1;
	}
	/* 2. 新建节点并初始化 */
	p = (hslinkedlink)malloc(sizeof(hslinkednode));
	if(p == NULL)
	{
		printf("The new hash list node malloc failed!\n");
		return -1;
	}
	p->key = key;
	p->value = key % N;
	p->next = NULL;
	/* 3. 插入节点 */
	q = &(HP->data[p->value]);
	/* 有序插入，从小到大 */
	while((q->next !=NULL) && (q->next->key < p->key))
	{
		q = q->next;
	}
	
	/* 4. 插入节点 */
	p->next = q->next;
	q->next = p;

	return 0;
}

5.4.3查找

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * @Function: hashlist_search
 * @Description: Hash表数据查询
 * @param HP: Hash表地址
 * @param key: 要查询的数据
 * @return  : 返回一个地址
 *            other,数据节点地址;
 *            NULL,Hash表不存在或者节点内存申请失败
 *
 */
hslinkedlink hashlist_search(hash * HP, data_h key)
{
	/* 定义一个Hash表节点结构体指针变量 */
	hslinkedlink p;
	/* 1. 判断Hash表是否存在 */
	if (HP == NULL)
	{
		printf(" hash list is not exited!\n");
		return NULL;
	}
	/* 2. 寻找Hash表key的存储位置的首节点 */
	p = &(HP->data[key % N]);
	/* 3. 查找数据 */
	while ((p->next !=NULL) && (p->next->key != key)) 
	{
		p = p->next;
	}
	/* 4. 判断是否查询到 */
	if (p->next == NULL) 
	{
		printf("The data is not in this hash list!\n");
		return NULL;
	} 
	else 
	{
		printf("The data is in this hash list!\n");
		return p->next;
	}

	return 0;
}

5.4.4显示

点击查看函数实现 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * @Function: hashlist_show
 * @Description: Hash表打印
 * @param HP: Hash表地址
 * @param key: 要查询的数据
 * @return  : 返回一个地址
 *            0,显示完成;
 *            -1,Hash表不存在
 *
 */
int hashlist_show(hash * HP)
{
	/* 定义一个Hash表节点结构体指针变量 */
	hslinkedlink p;
	int i = 0;
	/* 1. 判断Hash表是否存在 */
	if (HP == NULL)
	{
		printf(" hash list is not exited!\n");
		return -1;
	}
	/* 2. 访问Hash表 */
	for(i = 0; i < N; i++)
	{
		p = &(HP->data[i]);
		if(p->next != NULL)
		{
			printf("Hash data[%d]:", i);
			while(p->next != NULL)
			{
				printf("%d->",p->next->key);
				p = p->next;
			}
			puts("NULL");
		}	
		else
			printf("Hash data[%d]:NULL\n", i);
	}
	puts("");
	return 0;
}