LV05-02-H264-12-01-哥伦布编码
本文主要是哥伦布编码介绍的相关笔记,若笔记中有错误或者不合适的地方,欢迎批评指正😃。
点击查看使用工具及版本
| PC端开发环境 | Windows | Windows11 |
| Ubuntu | Ubuntu20.04.6的64位版本 | |
| VMware® Workstation 17 Pro | 17.0.0 build-20800274 | |
| 终端软件 | MobaXterm(Professional Edition v23.0 Build 5042 (license)) | |
| Win32DiskImager | Win32DiskImager v1.0 |
点击查看本文参考资料
点击查看相关文件下载
| --- | --- |
一、熵编码
1. 什么是熵?
熵在热力学中,是表示分子状态混乱程度的物理量,这时的熵称为热熵。后来信息论之父香农(C. E. Shannon)把“熵”这一词引入到信息论中,称为“信息熵”,信息越是随机,它的熵值越高。信息熵也是我们在h264这样的数字图像编码中使用的概念。因为我们待编码的图像像素信息、码流的各个句法元素值,其实都属于信息。
而信息熵,就是为了解决信息的量化度量问题,它描述了整个信源的平均信息量。信息熵在我们的熵编码中,表示了信源无损编码后平均码长的下限。所以我们上面才说,熵编码就是为了使编码后,码字的平均码长尽量达到熵极限。而且平均码长越接近熵,说明熵编码的压缩效率越高。
2. 什么是熵编码?
熵编码是无损编码的一种方法。该编码方法的宗旨是找到一种编码,使得码字的平均码长达到熵极限。具体实施是,对出现概率较大的符号,取较短的码长,对出现概率较小的符号取较大的码长。
3. 熵编码分类
3.1 变长编码
(1)香农范诺编码
(2)哈夫曼编码
(3)指数哥伦布编码
(4)CAVLC
3.2 算术编码
CABAC等。
二、哥伦布编码
1. 前言
在计算机中,一般数字的编码都为二进制,但是由于以相等长度来记录不同数字,因此会出现很多的冗余信息,如下:
| 十进制 | 5 | 4 | 255 | 2 | 1 |
|---|---|---|---|---|---|
| 二进制 | 00000101 | 00000100 | 11111111 | 00000010 | 00000001 |
| 有效字节 | 3 | 3 | 8 | 2 | 1 |
如数字1,原本只需要1个bit就能表示的数据,如今需要8个bit来表示,那么其余7个bit就可以看做是冗余数据,在网络传输时,如果以原本等长的编码方式来传输数据,则会出现很大的冗余量,加重网络负担。但是如果只用有效字节来传输上述码流,则会是:101 100 11111111 10 1,这样根本不能分离出原本的数据。
哥伦布编码则是作为一种压缩编码算法,能很有效地对原本的数据进行压缩,并且能很容易地把编码后的码流分离成码字。
2. 编码基本思想
一个码字的信息量,称之为熵,二进制上可用log2[n]来表示,也就是上面表格的有效字节,但是如果只是把有效码字串联起来,得到的只是一串无用的码流,因为这串码流中并没有描述单一码字的信息量,也就是无法对码流进行分离。
哥伦布编码就采用了加0前缀,用于表达码字的信息量,在得到N个0前缀后,就能知道该码字在码流中的长度,并从码流中把码字分离出来。
3. 哥伦布码
哥伦布码就是将编码对象分能成等间隔的若干区间(Group),每个Group有一个索引值:Group Id。对于Group Id采用一元码编码;对于Group内的编码对象采用定长码。如下图:
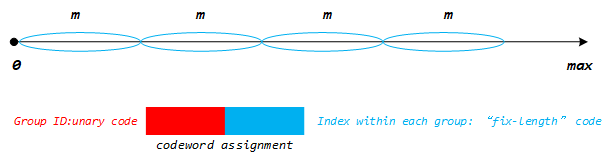
对于任一待编码的非负正整数N,Golomb编码将其分为两个部分:所在组的编号GroupID以及分组后余下的部分,GroupID实际是待编码数字N和参数m的商,余下的部分则是其商的余数,具体计算如下:
1 | #对于编码对象n |
Tips:
Golomb编码是一种无损的数据压缩方法,由数学家Solomon W.Golomb在1960年代发明。Golomb编码只能对非负整数进行编码,符号表中的符号出现的概率符合几何分布(Geometric Distribution)时,使用Golomb编码可以取得最优效果,也就是说Golomb编码比较适合小的数字比大的数字出现概率比较高的编码。它使用较短的码长编码较小的数字,较长的码长编码较大的数字。
三、编码原理
哥伦布编码使用指定的整数 M 把输入的整数分成两部分:商数 q、余数 r。 商数当做一元编码,而余数放在后面做为可缩短的二进制编码。
1. 一元编码
一元编码(Unary coding)是一种简单的只能对非负整数进行编码的方法,对于任意非负整数num,它的一元编码就是num个1后面紧跟着一个0。例如:
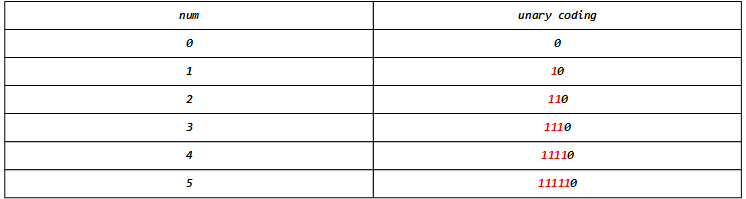
编解码的伪代码如下:
1 | UnaryEncode(n) { |
2. 余数处理
对于余下的部分r则有根据编码数字大小的不同有不同的处理方法。
- 如果参数m是2的次幂(Golomb-Rice编码)
使用取r的二进制表示的低log2(m) 位,作为r的码字。
- 如果m不是2的次幂
设 b = ⌈ log2(m)⌉,这里时若 r < 2^b - m,则使用b-1位的二进制编码r;若 r ≥ 2^b - m,则使用b位二进制对 r + 2^b -m 进行编码。
Tips:
⌈ a ⌉表示大于 a 的最小整数的ceil运算。
例如,m=5时,有:
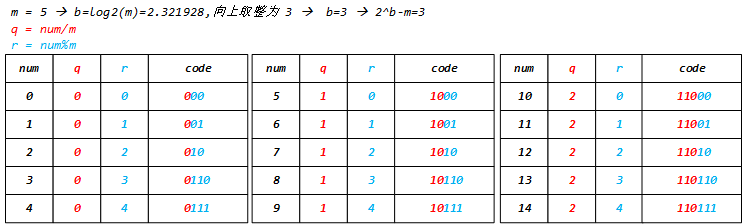
3. 总结
设待编码的非负整数为N,Golomb编码流程如下:
(1)初始化正整参数m;
(2)取得组号q以及余下部分r,计算公式为:q = N/m,r = N%m;
(3)使用一元编码的方式编码q;
(4)使用二进制的方式编码r。如果参数m是2的次幂(Golomb-Rice编码,指数哥伦布编码),使用取r的二进制表示的低log2(m) 位,作为r的码字;如果m不是2的次幂,设 b = ⌈ log2(m)⌉,若 r < 2^b - m,则使用b-1位的二进制编码r;若 r ≥ 2^b - m,则使用b位二进制对 r + 2^b -m 进行编码。
四、Golomb-Rice 编码
1. Golomb-Rice 编码是什么
Golomb-Rice是Golomb编码的一个变种,它给Golomb编码的参数m添加了个限制条件:m必须是2的次幂。这样有两个好处:
(1)不需要做模运算即可得到余数r:r = N & (m - 1);
(2)对余数r的编码更简单,只需要取r的二进制的低log2(m)位即可。
2. 总结
Golomb-Rice的编码过程更为简洁:
(1)初始化正整数m,m必须为2的次幂。
(2)计算q和r:q = N/m,r = N & (m - 1)。
(3)使用一元编码编码q。
(4)取r的二进制的低log2(m)作为r的码字。
五、指数哥伦布编码
1. 什么是指数哥伦布编码?
Rice的编码方式和Golomb的方法是大同小异的,只是选择m必须为2的次幂。而Exp-Golomb则有了一个很大的改进,不再使用固定大小的分组,而使组的大小呈指数增长。如下图:
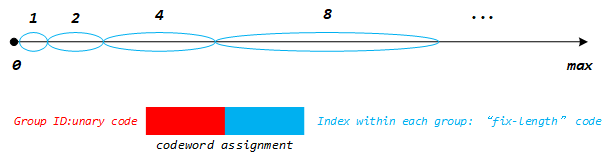
Exp-Golomb的码元结构是:
1 | [M zeros prefix] [1] [Offset] |
其中M是分组的编号GroupID,1可以看着是分隔符,Offset是组内的偏移量。
2. K阶Exp-Golomb
Exp-Golomb需要一个非负整数K作为参数,称之为K阶Exp-Golomb。其中当K = 0时,称为0阶Exp-Golomb,目前比较流行的H.264视频编码标准中使用的就是0阶的Exp-Golomb,并且可以将任意的阶数K转为0阶Exp-Golomb编码。
参考资料: