LV01-01-C语言-数据类型

发表于 分类于 ， ， 本文字数： 10k 阅读时长 ≈ 37 分钟

本文主要是C语言基础——数据类型相关笔记，若笔记中有错误或者不合适的地方，欢迎批评指正😃。

点击查看使用工具及版本
Windows windows11
Ubuntu Ubuntu16.04的64位版本
VMware® Workstation 16 Pro 16.2.3 build-19376536
SecureCRT Version 8.7.2 (x64 build 2214) - 正式版-2020年5月14日
开发板 正点原子 i.MX6ULL Linux阿尔法开发板
uboot NXP官方提供的uboot，NXP提供的版本为uboot-imx-rel_imx_4.1.15_2.1.0_ga(使用的uboot版本为U-Boot 2016.03)
linux内核 linux-4.15(NXP官方提供)
STM32开发板 正点原子战舰V3(STM32F103ZET6)
点击查看本文参考资料
参考方向 参考原文
------
点击查看相关文件下载
--- ---

一、数据的形式

计算机要处理大量的信息，如数字、文字、符号、图形、音频、视频等，这些信息对于计算机来说，都是一样的，都是以二进制的形式来表示。

内存条是一个非常精密的部件，包含了上亿个电子元器件。这些元器件，实际上就是数字电路；数字电路的电压会变化，但是却只有两种状态要么是高电平（如 5.0V 、 3.3V 等），要么是低电平（如 0V ）。 1 代表高电平， 0 代表低电平，这样就得到了元器件的两种状态。元器件组合在一起的时候，便产生许多不同的组合。例如， 8 个元器件有 256(2的8次方) 种不同的组合， 16 个元器件有 65536(2的16次方) 种不同的组合。

1 个元器件称为 1 比特（ Bit ）或 1 位， 8 个元器件称为 1 字节（ Byte ）

点击查看计算机内存单位换算 
1
2
3
4
5
6
7
1Byte = 8 Bit
1KB = 1024Byte
1MB = 1024KB
1GB = 1024MB
1TB = 1024GB
1PB = 1024TB
1EB = 1024PB

计算机只认识 0 和 1 两个数字，所以一切东西在计算机内部都会转化为 0 和 1 的组合。但是我们写程序不可能使用 0 和 1 来写吧，后来出现了汇编， C 语言等等很多的编程语言。这样我们才能很方便的与计算机进行”交流”。

二、数据表示

1. 数值数据

数值型的数据在内存中最终都是以二进制的形式表示的，后边会有详细说明。

十进制 二进制 八进制 十六进制
0 0000 0 0
1 0001 1 1
2 0010 2 2
3 0011 3 3
4 0100 4 4
5 0101 5 5
6 0110 6 6
7 0111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 a
11 1011 13 b
12 1100 14 c
13 1101 15 d
14 1110 16 e
15 1111 17 f

2. 非数值数据( ASCII )

非数值型的数据，部分会转换为 ASCII 码来存储，后边会有详细说明。

1641269764160

二、数据类型

1. 数据类型及标识符

分类 数据类型 标识符
基本类型 整型 int(基本整形)
long(长整型)
short(短整型)
unsigned(无符号整型)
字符型 char
浮点型 float(单精度)
double(双精度)
枚举型 enum
构造类型 结构体类型 struct
共用体类型 union
数组 基本类型和构造类型组成数组
空类型 空类型 void
指针类型 指针类型 *

2. 数据类型长度

一种数据类型占用的字节数，称为该数据类型的长度。例如， short 占用 2 个字节的内存，那么它的长度就是 2 。

常用数据类型 16位平台 32位平台 64位平台
字节数 位数 字节数 位数 字节数 位数
char
unsigned char		 1 8 1 8 1 8
short
unsigned short		 2 16 2 16 2 16
int
unsigned int		 2 16 4 32 4 32
long
unsigned long		 4 32 4 32 8 64
long long --- --- 8 64 8 64
指针 2 16 4 32 8 64
bool 1 8 1 8 1 8
float 4 32 4 32 4 32
double 8 64 8 64 8 64

3. 定点数与浮点数

3.1 定点数

数字既包括整数，又包括小数，而小数的精度范围要比整数大得多，所以如果我们想在计算机中，既能表示整数，也能表示小数，关键就在于这个小数点。

于是人们便与计算机约定小数点的位置，且这个位置固定不变。小数点前、后的数字，分别用二进制表示，然后组合起来就可以把这个数字在计算机中存储起来。用这种方法表示的数字叫做定点数。

定点数如果要表示整数或小数，分为以下三种情况：

纯整数例如：100，小数点其实在最后一位，所以忽略不写
纯小数例如：0.125，小数点固定在最高位
整数+小数 例如：1.28、32.35，小数点在指定某个位置
点击查看实例
  • 纯整数
1
2
/* 以 1 个字节（8 bit）表示 */
100(D) = 0110 0100(B)
  • 纯小数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 以 1 个字节（8 bit）表示 */
0.125(D) = 0.0010 0000(B)
    
/* ==============================    
0.125 x 2 = 0.250 ----- 取0剩0.250
0.250 x 2 = 0.500 ----- 取0剩0.500
0.500 x 2 = 1.000 ----- 取1剩0.000
0.000 x 2 = 0.000 ----- 取0剩0.000
    
0.000 x 2 = 0.000 ----- 取0剩0.000
0.000 x 2 = 0.000 ----- 取0剩0.000
0.000 x 2 = 0.000 ----- 取0剩0.000
所以最后就是 0.0010 0000
 * ============================== */

【说明】小数转二进制方法：乘 2 取整，一直乘到要求的位数。

  • 整数+小数

我们需要先约定小数点的位置。依旧以 1 个字节（ 8 bit ）为例，我们可以约定前 5 位表示整数部分，后 3 位表示小数部分。

1
2
3
/* 以 1 个字节（8 bit）表示 */
/* 前5位表示整数部分，后3位表示小数部分 */
25.125(D) = 11001 001(B)

用定点格式来存储小数，优点是精度高，因为所有的位都可以用来存储有效数字。缺点是取值范围太小，不能表示很大或者很小的数。

3.2 浮点数

在实际问题中，有很多数据的数量级特别大，小数的取值范围很大，最大值和最小值的差距有上百个数量级，使用定点数来存储将变得非常困难。例如，

$$
2000000000000000000000000000000000 g = 2 × 10^{33} g
$$
这用科学计数法很容易表示，但是计算机中怎么办，没有这么大的数据类型吧。如果真要存，那将会需要很大的一块内存，估计要几十个字节。那计算机不能也学习一下科学计数法吗🤣？用指数来存储不好吗？

于是，这种以指数的形式来存储小数的解决方案就叫做浮点数。浮点数克服了定点数取值范围太小的缺点。

4. 整数

C 语言使用定点数格式来存储 short 、 int 、 long 类型的整数，定点数中的点指的就是小数点。对于整数，可以认为小数点后面都是零。

4.1 常见的整型

现在的操作系统中， int 一般占用 4 个字节（ Byte ）的内存，共计 32 位（ Bit ）。使用 4 个字节保存较小的整数绰绰有余，我们正常使用的时候，一般会空闲出两三个字节来，这些字节就白白浪费掉了，不能再被其他数据使用。在单片机和嵌入式系统中，内存都是非常稀缺的资源，所有的程序都在尽力节省内存。

让整数占用更少的内存可以在 int 前边加 short ，让整数占用更多的内存可以在 int 前边加 long 。 short 、 int 、 long 是 C 语言中常见的整数类型，其中 int 称为整型， short 称为短整型， long 称为长整型。

4.2 整型的长度

对于上边说三种整型来说，只有 short 的长度是确定的，是两个字节，而 int 和 long 的长度无法确定，在不同的环境下可能会有所不同。C语言并没有严格规定 short 、 int 、 long 的长度，只做了宽泛的限制：

  • （1）short 至少占用2个字节。

  • （2）short 的长度不能大于 int。

  • （3）long 的长度不能小于 int。

总的来说，它们的长度(所占字节数)关系为：short <= int <= long。这说明 short 并不一定真的” 短 “，long也并不一定真的” 长 “，它们有可能和 int 占用相同的字节数。

在16位环境下，short为2个字节，int为2个字节，long为4个字节。对于32位的Windows、Linux和OSX，short为2个字节，int为4个字节，long也为4个字节。在64位环境下，不同的操作系统会有不同的结果，具体如下所示(长度以字节计)：Windows 64位系统： short为2字节、 int为4字节， long 为4字节。类Unix系统(包括Unix、Linux、OSX、BSD、Solaris等)： short为2字节、 int为4字节， long为8字节。

4.3 整型的输出

后边我们会接触到 printf 函数来输出一些数据，对于整数来说，常用的格式控制符如下：

%hd输出 short int 类型，hd 是 short decimal 的简写；
%d输出 int 类型，d 是 decimal 的简写；
%ld输出 long int 类型，ld 是 long decimal 的简写。

4.4 整数的符号？

整数，自然会有正负之分，那正负怎么界定呢？C 语言规定，把内存的最高位作为符号位。以 int 为例，它占用 32 位的内存， 0~30 位表示数值， 31 位表示正负号。最高位是 1 表示为负数，最高位是 0 表示为正数。

image-20220330170351148

short 、 int 和 long 类型默认都是带符号位的，符号位以外的内存才是数值位。如果只考虑正数，那么各种类型能表示的数值范围（取值范围）就比原来小了一半。

但是我们很多时候可以确定某个数字只能是正数，比如，人数、字符串的长度、内存地址等，这个时候符号位就是多余的了，那我们就可以删掉符号位，把所有的位都用来存储数值，这样能表示的数值范围更大（大一倍）。 C 语言中通过 unsigned 表示没有符号位，于是就出现了 unsigned short 、 unsigned int 、 unsigned long 。

4.5 整数的存储

对于有符号数，都是以补码的形式存于内存中。那什么是补码，为什么要用补码呢？

4.5.1 几个基本概念

  • 机器数

机器数就是一个数在计算机中的二进制表示，计算机中机器数的最高位是符号位，正数符号位为 0 ，负数符号位为 1 。机器数包含原码、反码和补码三种表示形式。如：数字 3 若用 8 位二进制数表示，则机器数为 0000 0011 ，数字 -3 若用 8 位二进制数表示，则机器数为 1000 0011 。

  • 机器数的真值

真值就是带符号位的机器数对应的真正数值。如：机器数为 0000 0011 则，真值为 3 ，机器数为 1000 0011 ，则真值为 -3 。

4.5.2 原码、反码、补码

  • 原码

若机器字长为 n ，那么一个数的原码就是用一个 n 位的二进制数表示出来的机器数，其中最高位为符号位：正数为 0 ，负数为 1 ，位数不够的用 0 补全。其实就是 原码 = 符号位(0或1) + 真值的绝对值 。如（假设机器字长为 8 ）： 3 的原码为 0000 0011 ， -3 的原码为 1000 0011 。

【注意】 0 的原码有两个： [+0] 原码为 0000 0000 ； [-0] 原码为 1000 0000 。

  • 反码

正数的反码就是其本身，负数的反码为除了符号位不变外，其他各位取反。如（假设机器字长为 8 ）： 3 的反码为 0000 0011 ， -3 的反码为 1111 1100 。

【注意】 0 的反码有两个： [+0] 反码为 0000 0000 ； [-0] 反码为 1111 1111 。

  • 补码

正数的补码就是其本身，负数的补码则是反码加一。如（假设机器字长为 8 ）： 3 的补码为 0000 0011 ， -3 的补码为 1111 1101 。

【注意】：

（1）0 的补码只有一个： [0] 补码为 0000 0000 。

（2）在8 位数据长度下 -128 ，没有原码和反码，补码为 10000000 。

4.5.3 为什么使用反码和补码

在使用原码进行计算的时候，对于人来说，可以轻易识别符号位，轻松知道正负，然后再对其他位来进行计算，对于计算机的设计来说，识别符号位就是一项复杂的工程了，若是能让符号位直接参与计算，那么这样就可以忽略符号位的识别了。

对于加法来说，符号位有没有影响不大，但是对于减法来说，计算机是将其转换为加法来进行运算，所以若是通过原码来进行计算（符号位直接参与计算）则：

1
2
3
4
5
5 - 3 = 2
      = 5 + (-3)
      = 0000 0101(原码) + 1000 0011(原码)
      = 1000 1000(原码)
      = -8

显然，计算结果理论上为 2 ，但是计算机按照原码计算出来的数值为 -8 ，所以对减法来说，原码计算的方式不行，于是引入反码，若通过反码进行减法计算，则有：

1
2
3
4
5
6
7
8
9
5-3 = 2
    = 5 + （-3）
    = 0000 0101（原码） + 1000 0011（原码）
    = 0000 0101（反码） + 1111 1100（反码）
    = 1 0000 0001（反码）
    = 0000 0001（反码） + 0000 0001（高位进位，结果要加1）
    = 0000 0010（反码，符号位为0，为正数）
    = 0000 0010（原码）
    = 2

【注意】反码计算的运算规则：从低到高位逐列进行计算。 0+0=0,0+1=1,1+1=0(向高位进1) 。若最高位产生了进位，则最后得到的结果要加1。

但是，有一个问题出现了对于相同两个数相减，如：

1
2
3
4
5
6
7
1 - 1 = 0
      = 1 + (-1) 
      = 0000 0001(原码) + 1000 0001(原码) 
      = 0000 0001(反码) + 1111 1110
      = 1111 1111(反码)
      = 1000 0000(原码)
      = -0

显然，计算出的结果的真值是对的，但是结果却是 -0 ，通过上边已经知道 0 的原码和反码都有2个，所以，用反码进行计算时遇上了 0 ，这样的结果就是不合理的了，于是，又引入了补码，则：

1
2
3
4
5
6
7
8
9
1 - 1 = 0
      = 1 + (-1)
      = 0000 0001(原码) + 1000 0001(原码)
      = 0000 0001(反码) + 1111 1110(反码)
      = 0000 0001(补码) + 1111 1111(补码)
      = 1 0000 0000(补码)
      = 0000 0000(补码，最高位进位，舍去进位)
      = 0000 0000(最高位为0，是正数)
      = 0

这样计算结果就没得问题了。

【注意】补码计算时，若最高位产生进位，则舍去进位，注意与反码相区别。

5. 小数

整数是以定点数的形式存储，那么小数呢？

5.1 表示形式

小数在内存中是以浮点数的形式存储的。使用浮点数格式来存储 float 、 double 类型的小数。C 语言标准规定，小数在内存中转换为科学计数法的形式，然后进行存储，具体形式为：

$$
flt = (-1)^{sign} × mantissa × base^{exponent}
$$

flt要表示的小数。
sign表示 flt 的正负号，它的取值只能是 0 或 1：取值为 0 表示 flt 是正数，取值为 1 表示 flt 是负数。
base基数，或者说进制，它的取值大于等于 2（例如，2 表示二进制、10 表示十进制、16 表示十六进制……）。数学中常见的科学计数法是基于十进制的，例如 6.93 × 1013；计算机中的科学计数法可以基于其它进制，例如 1.001 × 27 就是基于二进制的，它等价于 1001 0000。
mantissa尾数，或者说精度，是 base 进制的小数，并且 1 ≤ mantissa < base，这意味着，小数点前面只能有一位数字；
exponent指数，是一个整数，可正可负，并且为了直观一般采用十进制表示。
点击查看实例

以 19.625 为例，我们现在就将小数转换为浮点格式。

  • base = 10

根据上边的表格，可以知道：

1
2
3
4
sign = 0
mantissa = 1.9625
base = 10
exponent = 1

所以有：
$$
19.625 = 1.9625 × 10^1
$$

  • base = 2

先将 19.625 转换为二进制表示的形式 1 0011.101 。

点击查看转换说明 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 整数部分 19 */
19 / 2 = 9 ... 1 ----- 取 1 剩 9
9 / 2 = 4 ... 1  ----- 取 1 剩 4
4 / 2 = 2 ... 0  ----- 取 0 剩 2
2 / 2 = 1 ... 0  ----- 取 0 剩 1
1 / 2 = 0 ... 1  ----- 取 1
所以19(D) = 10011(B)
/* 小数部分 0.625 */
0.625 x 2 = 1.250 ----- 取 1 剩 0.250
0.250 x 2 = 0.500 ----- 取 0 剩 0.500
0,500 x 2 = 1.000 ----- 取 1 剩 0.000
所以0.625(D) = 101(B)

故 19.625(D) = 1 0011.101(B)

有以下形式：
$$
19.625 = 1×2^4 + 0×2^3 + 0×2^2 + 1×2^1 + 1×2^0 + 1×2^{-1} + 0×2^{-2} + 1×2^{-3}
$$
根据上边的表格，可以知道：

1
2
3
4
5
19.625 = 1 0011.101
sign = 0
mantissa = 1.0011101
base = 2
exponent = 4

所以有：
$$
19.625 = 1 0011.101 =1.0011101 × 2^4
$$

【说明】当基数（进制） base 确定以后，指数 exponent 实际上就是小数点的移动位数：

  • exponent 大于零， mantissa 中的小数点右移 exponent 位即可还原小数的值；
  • exponent 小于零， mantissa 中的小数点左移 exponent 位即可还原小数的值。

5.2 内存分配

C 语言中常用的浮点数类型为 float 和 double 。其中 float 始终占用 4 个字节， double 始终占用 8 个字节。浮点数存储时的内存被分成三部分，分别用来存储符号 sign 、尾数 mantissa 和指数 exponent ，当浮点数的类型确定后，每一部分的位数就是固定的。

image-20220331190334664

5.3 存储方式

在计算及内部，小数也会被转化为二进制，那么二进制的浮点数是如何存储的呢？

5.3.1 符号的存储

符号的存储与整数类似，单独分配出一个位（ Bit ）来，用 0 表示正数，用 1 表示负数。

5.3.2 尾数的存储

还是以 19.625 为例，我们上边已经知道了转换后的尾数部分为 1.0011101 。

小数转换为浮点格式的二进制数后，尾数部分的取值范围为 1 ≤ mantissa ＜ 2 ，这说明尾数的整数部分一定为 1 ，是一个恒定的值，这样就无需在内存中体现出来，可以将其直接截掉，只要把小数点后面的二进制数字放入内存中即可。

对于 1.0011101 ，就是把 0011101 放入内存就可以了。

如果 base 采用其它进制，那么尾数的整数部分就不是固定的，它有多种取值的可能，以十进制为例，尾数的整数部分可能是 1~9 之间的任何一个值，这样一来尾数的整数部分就不能省略了，必须在内存中体现出来。所以将 base 设置为二进制就可以节省掉一个位（ Bit ）的内存，

5.3.3 指数的存储

指数是一个整数，它有正负之分，所以我们不仅需要存储值，还要存储符号。

short 、 int 、 long 等类型的整数在内存中的存储采用的是补码加符号位的形式，数值在写入内存之前必须先进行转换，读取以后还要再转换一次。但是为了提高效率，避免繁琐的转换，指数的存储并没有采用补码加符号位的形式。那是怎么进行的呢？

以 float 为例，它的指数部分占 8 位，可以表示 0~255 的值。

image-20220331190408975

那么我们就取中间值 127 ，指数在写入内存前先加上 127 ，读取时再减去 127 ，此时正负就很容易区分了。

点击查看中间值取法

设中间值为 median ，指数部分占用的内存为 n 位，那么中间值的计算方法如下：
$$
median = 2^{n-1} - 1
$$
对于 float ，中间值为 $2^{8-1} - 1 = 127$；对于 double ，中间值为 $2^{11-1} -1 = 1023$。

我们可以将内存中存储的指数命名为 exp ，那么有内存中的指数等于真实指数加上中间值，即：
$$
exp = exponent + median
$$

例如 19.625 转换后的指数为 4 ，用 4 加上 127 ，结果就是 131 ，转换为二进制就是 1000 0011 ，这就是指数部分在内存中二进制形式。

5.4 验证存储方式

小数的存储还是比较复杂的，我们可以来验证一下，后边我们会学习到结构体，也会接触到位域。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
/* 浮点数结构体 */
/* 小端模式下，靠下的为高位，靠上的为低位*/
typedef struct Float_data
{
	unsigned int nMant : 23;  /* 尾数部分 */
    unsigned int nExp : 8;    /* 指数部分 */
	unsigned int nSign : 1;   /* 符号位 */ 
}FP_SINGLE;

int main(int argc, const char *argv[]) 
{
    float temp = 19.625;
    FP_SINGLE *p = (FP_SINGLE*)&temp;
   
    printf("sign: %x\n", p->nSign);
    printf("exp: %x\n", p->nExp);
    printf("mant: %x\n", p->nMant);

    return 0;
}

然后在命令行运行以下命令：

1
2
gcc test.c -Wall
./a.out

会看到以下输出：

1
2
3
sign: 0
exp: 83
mant: 1d0000

我们无法打印二进制数据，但是可以用十六进制数代替，换算一下即可：

1
2
3
sign: 0
exp: 83 = 1000 0011
mant: 1d0000 = 0001 1101 0000 0000 0000 0000

6. 字符

之前的时候，我一直以为 C 语言中的字符都是以 ASCII 码的形式存储在内存中，但是后来发现，不仅仅是这样。在 C 语言中，只有 char 类型的窄字符才使用 ASCII 编码， char 类型的窄字符串、 wchar_t 类型的宽字符和宽字符串都不使用 ASCII 编码。

6.1 ASCII 码

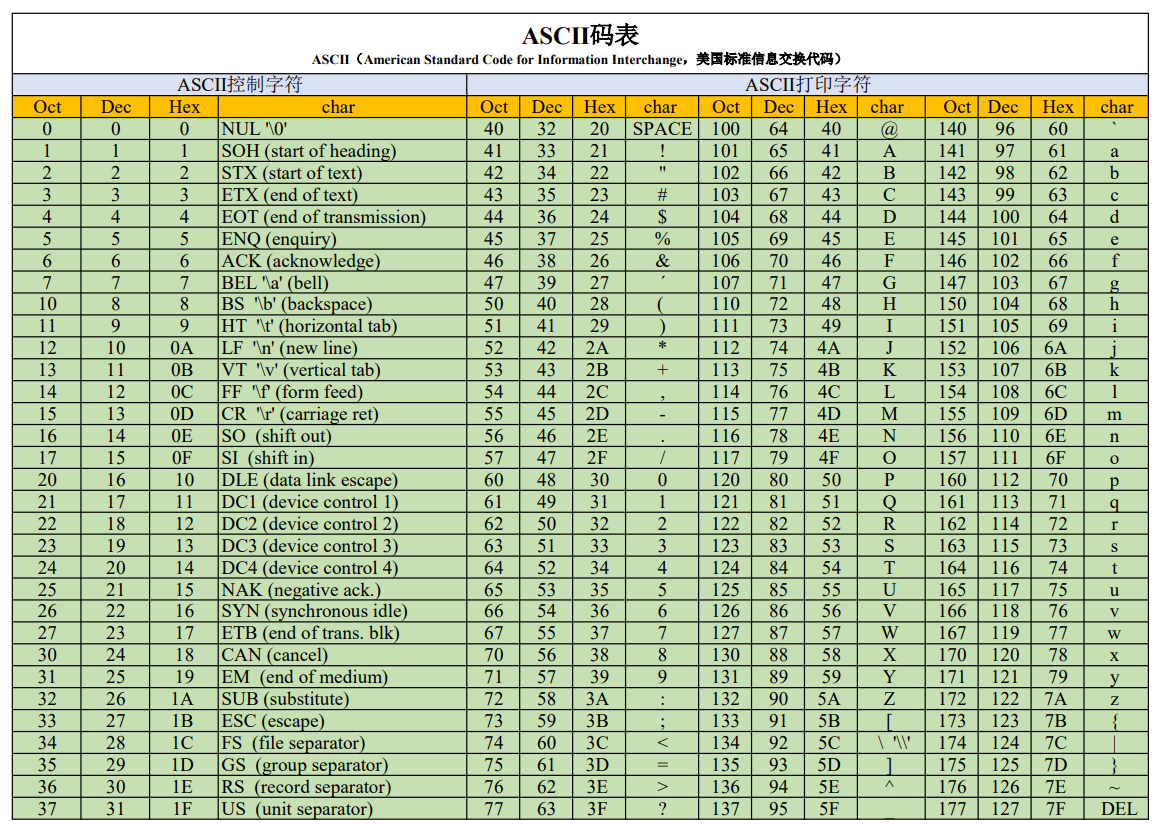
上边我们已经见识了一张 ASCII 码表，那么这究竟是什么呢？

一个二进制位( Bit )有 0 和 1 两种状态，一个字节( Byte )有 8 个二进制位，有 256 种状态，每种状态对应一个符号，就是 256 个符号，从 0000 0000 到 1111 1111 。

计算机也只认识 0 和 1 ，那么对于字符来说也就需要转化为二进制的形式了。当初计算机是诞生于美国，在考虑计算机显示文字的问题时，美国制定了一套英文字符与二进制位的对应关系，称为 ASCII （ American Standard Code for Information Interchange ，美国信息交换标准代码）。

标准 ASCII 码规定了 128 个英文字符与二进制的对应关系，占用一个字节（实际上只占用了一个字节的后面 7 位，最前面 1 位统一规定为 0 ），这一位被称为奇偶校验位。后边的 128 个被称为扩展 ASCII 码。

点击查看什么是奇偶校验位

所谓奇偶校验，是指在代码传送过程中用来检验是否出现错误的一种方法，一般分奇校验和偶校验两种。奇校验规定：正确的代码一个字节中 1 的个数必须是奇数，若非奇数，则在最高位 b7 添 1 ；偶校验规定：正确的代码一个字节中 1 的个数必须是偶数，若非偶数，则在最高位 b7 添 1 。

6.2 宽字符与窄字符

上边我们提到了宽字符和窄字符，这又是什么呢？宽窄字符是与一个字符所占的字节数有关，如果一个字符只占 1 个字节，那么它就是窄字符，一个宽字符通常占 2 个字节。在 C 语言中， char 类型就是占 1 个字节，它属于窄字符，这种类型的字符可以与 ASCII 一一对应。

我们在以往的编程中，会发现，在 C 语言中是可以使用中文的，但是我们的中文可是远远多于 256 的，也用 ASCII 来对应的话，显然是不可能的。那么中文怎么存储呢？

6.3 宽字符的存储

C 语言是一门全球化的编程语言，它支持世界上任何一个国家的语言文化，包括中文、日语、韩语等。只是我们使用英文更多些罢了，而且似乎也会更方便些。上边我们提到了一个问题，那就是中文字符怎么存储，其实不仅仅是中文字符，除了 char 类型的窄字符，那些宽字符怎么存储呢？

点击查看需要解决的三个问题
  • （1）足够长的数据类型

char 只能处理 ASCII 编码中的英文字符，是因为 char 类型太短，只有一个字节，容纳不下我们的几万个汉字，要想处理中文字符，必须得使用更长的数据类型。

一个字符在存储之前会转换成它在字符集中的编号，而这样的编号是一个整数（就类似于 ASCII 码），所以我们可以用整数类型来存储一个字符，比如 unsigned short 、 unsigned int 、 unsigned long 等。

  • （2）选择包含中文的字符集

C 语言规定，对于汉语等 ASCII 编码之外的单个字符，也就是专门的字符类型，要使用宽字符的编码方式。常见的宽字符编码有 UTF-16 和 UTF-32 ，它们都是基于 Unicode 字符集的，能够支持全球的语言文化。

点击查看 Unicode 简介

Unicode 编码则是采用双字节 16 位来进行编号，可编 65536 字符，基本上包含了世界上所有的语言字符，它也就成为了全世界一种通用的编码。

在真正实现时，微软编译器（内嵌于 Visual Studio 或者 Visual C++ 中）采用 UTF-16 编码，使用 2 个字节存储一个字符，用 unsigned short 类型就可以容纳。 GCC 、 LLVM/Clang （内嵌于 Xcode 中）采用 UTF-32 编码，使用 4 个字节存储字符，用 unsigned int 类型就可以容纳。

  • （3）跨平台

不同的编译器可以使用不同的整数类型。如果代码使用 unsigned int 来存储宽字符，那么在微软编译器下就是一种浪费；如果代码使用 unsigned short 来存储宽字符，那么在 GCC 、 LLVM/Clang 下就不够。

为了解决上边的问题， C 语言推出了一种新的类型，叫做 wchar_t 。 w 是 wide 的首字母， t 是 type 的首字符， wchar_t 的意思就是宽字符类型。

wchar_t 长度

wchar_t 的长度由编译器决定：

  • 在微软编译器下，它的长度是 2 ，相当于 unsigned short ；
  • 在 GCC 、 LLVM/Clang 下，它的长度是 4 ，相当于 unsigned int 。

6.4 宽字符的使用

wchar_t 类型位于 <wchar.h> 头文件中，它使得代码在具有良好移植性的同时，也节省了不少内存。要想使用宽字符的编码方式，就得加上 L 前缀，加上 L 前缀后，所有的字符都将成为宽字符，占用 2 个字节或者 4 个字节的内存，包括 ASCII 中的英文字符。

点击查看实例 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
#include <wchar.h>
#include <locale.h> /* setlocale函数 */

int main(int argc, const char *argv[]) 
{
	/* 将本地环境设置为 UTF-8 简体中文 */
    setlocale(LC_ALL, "zh_CN.UTF-8");
    wchar_t a = L'A';  //英文字符（基本拉丁字符）
	wchar_t b = L'9';  //英文数字（阿拉伯数字）
	wchar_t c = L'繁';  //中文汉字
	wchar_t d = L'华';  //中文汉字
	wchar_t e = L'。';  //中文标点
	wchar_t f = L'♥';   //特殊符号
	wchar_t g = L'༄';  //藏文

	wprintf(L"Wide chars: %lc %lc %lc %lc %lc %lc %lc\n",  //必须使用宽字符串
        	a, b, c, d, e, f, g);

    return 0;
}

然后在命令行运行以下命令：

1
2
gcc test.c -Wall
./a.out

会看到以下输出：

1
Wide chars: A 9 繁 华 。 ♥ ༄

【注意】

（1）宽字符的输出要用到 wprintf 函数。

（2）注意设置语言环境，否则输出的可能全是 ? 。

四、源文件编码

上边了解了 C 语言中字符的编码，源文件也是存储在计算机中的，那源文件是什么编码呢？源文件最终会被存储到本地硬盘，或者远程服务器，这个时候就要尽量压缩文件体积，以节省硬盘空间或者网络流量，而代码中大部分的字符都是 ASCII 编码中的字符，用一个字节足以容纳，所以 UTF-8 编码是一个不错的选择。

UTF-8 兼容 ASCII ，并且 UTF-8 基于 Unicode ，支持全世界的字符。常见的 IDE 或者编辑器，例如 Xcode 、 Gedit 、 Vim 等，在创建源文件时一般也默认使用 UTF-8 编码。

还有一种是本地编码，所谓本地编码就是像 GBK 、 Big5 、 Shift-JIS 等这样的国家编码（地区编码）；针对不同国家发行的操作系统，默认的本地编码一般不同。简体中文版本的 Windows 默认的本地编码是 GBK 。 Visual Studio 就默认使用本地编码来创建源文件。

对于编译器来说，它往往支持多种编码格式的源文件。微软编译器、 GCC 、 LLVM/Clang （内嵌于 Xcode 中）都支持 UTF-8 和本地编码的源文件，微软编译器还支持 UTF-16 编码的源文件。如果考虑到源文件的通用性，就只能使用 UTF-8 和本地编码了。

五、常见编码方式

1. ASCII 码

前边介绍过了，它总共有 128 个，主要是用于窄字符的编码。

2. ISO-8859-1

ISO 组织在 ASCII 码基础上制定了一些列标准用来扩展 ASCII 编码，它们是 ISO-8859-1~ISO-8859-15 ，其中 ISO-8859-1 涵盖了大多数西欧语言字符，所有应用的最广泛。 ISO-8859-1 仍然是单字节编码，它总共能表示 256 个字符。

3. GB2312

全称是《信息交换用汉字编码字符集 基本集》，它是双字节编码，总的编码范围是 A1-F7 ，其中从 A1-A9 是符号区，总共包含 682 个符号，从 B0-F7 是汉字区，包含 6763 个汉字。

4. GBK  

全称叫《汉字内码扩展规范》，是国家技术监督局为 windows95 所制定的新的汉字内码规范，它的出现是为了扩展 GB2312 ，加入更多的汉字。

它的编码范围是 8140~FEFE （去掉 XX7F ）总共有 23940 个码位，它能表示 21003 个汉字，它的编码是和 GB2312 兼容的。

5. GB18030

全称是《信息交换用汉字编码字符集》，是我国的强制标准，它可能是单字节、双字节或者四字节编码，它的编码与 GB2312 编码兼容。

6. Unicode 字符集

前边也大致介绍了一下，这与 ASCII 很类似， Unicode 相当于一本很厚的字典，记录着世界上所有字符对应的一个数字。

它仅仅只是一个字符集，规定了符合对应的二进制代码，至于这个二进制代码如何存储则没有任何规定。

7. UTF-16

UTF-16 具体定义了 Unicode 字符在计算机中存取方法。 UTF-16 用两个字节来表示 Unicode 转化格式，这个是定长的表示方法，不论什么字符都可以用两个字节表示，两个字节是 16 个 bit ，所以叫 UTF-16 。

UTF-16 表示字符非常方便，每两个字节表示一个字符，这样在字符串操作时就大大简化了操作。

8. UTF-8

UTF-16 统一采用两个字节表示一个字符，虽然在表示上非常简单方便，但是有很大一部分字符用一个字节就可以表示的现，这样存储空间放大了一倍，珍贵的内存空间就被浪费掉了。

UTF-8 全称 8bit Unicode Transformation Format ， 8 比特的 Unicode 通用转换格式。它采用了一种变长技术,每个编码区域有不同的字码长度。不同类型的字符可以是由 1~6 个字节组成。 编码规则如下：

  • 对于单字节的符号, 字节的第一位（最高位，也就是第 8 位）设为 0 , 后面 7 位为这个符号的 unicode 码. 因此对于英语字母,来说， UTF-8 编码和 ASCII 码是相同的.

  • 对于 n 字节的符号( n > 1 ), 第一个字节的前 n 位都设为 1 ，第 n+1 位设为 0 ，后面剩余的 n - 1 个字节的前两位一律设为 10 。剩下的二进制位, 全部为这个符号的 Unicode 码.

nUnicode 十六进制码范围 UTF-8 二进制
10000 0000 - 0000 007F 0xxxxxxx
20000 0080 - 0000 07FF 110xxxxx 10xxxxxx
30000 0800 - 0000 FFFF 1110xxxx 10xxxxxx 10xxxxxx
40001 0000 - 0010 FFFF 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx
50020 0000 - 03FF FFFF 111110xx 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx
60400 0000 - 7FFF FFFF 1111110x 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx
【注意】在 UTF-8 编码中，英文字符占一个字节，中文字符占用 3 个字节。