LV03-02-数据结构-线性表-基础知识
本文主要是数据结构——线性表基础知识相关笔记,若笔记中有错误或者不合适的地方,欢迎批评指正😃。
点击查看使用工具及版本
| Windows | windows11 |
| Ubuntu | Ubuntu16.04的64位版本 |
| VMware® Workstation 16 Pro | 16.2.3 build-19376536 |
| SecureCRT | Version 8.7.2 (x64 build 2214) - 正式版-2020年5月14日 |
| 开发板 | 正点原子 i.MX6ULL Linux阿尔法开发板 |
| uboot | NXP官方提供的uboot,NXP提供的版本为uboot-imx-rel_imx_4.1.15_2.1.0_ga(使用的uboot版本为U-Boot 2016.03) |
| linux内核 | linux-4.15(NXP官方提供) |
| STM32开发板 | 正点原子战舰V3(STM32F103ZET6) |
点击查看本文参考资料
| 参考方向 | 参考原文 |
| --- | --- |
一、线性表的概念
线性表,全称其实是线性存储结构。它是一种一对一的逻辑关系,它是包含若干数据元素的一个线性序列。记为:
$$
L = (a_0, a_1, …, a_{i-1},a_i,a_{i+1}, …,a_{n-1})
$$
其中 L 称为表名,$a_i( 0 \le i \le n-1)$; n 为表长,当 n > 0 时,线性表 L 为非空表,否则为空表。
线性表还可以用二元组的形式表示:
$$
L = (D,R)
$$
其中:
- D 为数据元素集合
$$
D={a_i | a_i \in datatype ,i=0,1,2, ……, n-1 ,n\ge 0}
$$
- R 为关系集合
$$
R={<a_i , a_{i+1}> | a_i , a_{i+1} \in D, 0 \le i \le n-2}
$$
- 关系符$<a_i, a_{i+1}>$在这里称为有序对,表示任意相邻的两个元素之间的一种先后次序关系。
点击查看实例
设有一个线性表 L = {1, 2, 3, 4, 5} ,它们的关系如下图:

使用二元组 L = (D, R) 描述该线性表,则有:
1 | D={1 , 2 , 3 , 4 , 5} (n = 5) |
【注意】使用线性表存储的数据,如同向数组中存储数据那样,要求数据类型必须一致,一半是整形,另一半是字符串的一组数据无法使用线性表存储。
二、线性表存储结构
线性表可以理解为用一根线把数据按照顺序串起来,然后把这一串数据放置到物理空间,我们可以选择以下两种:
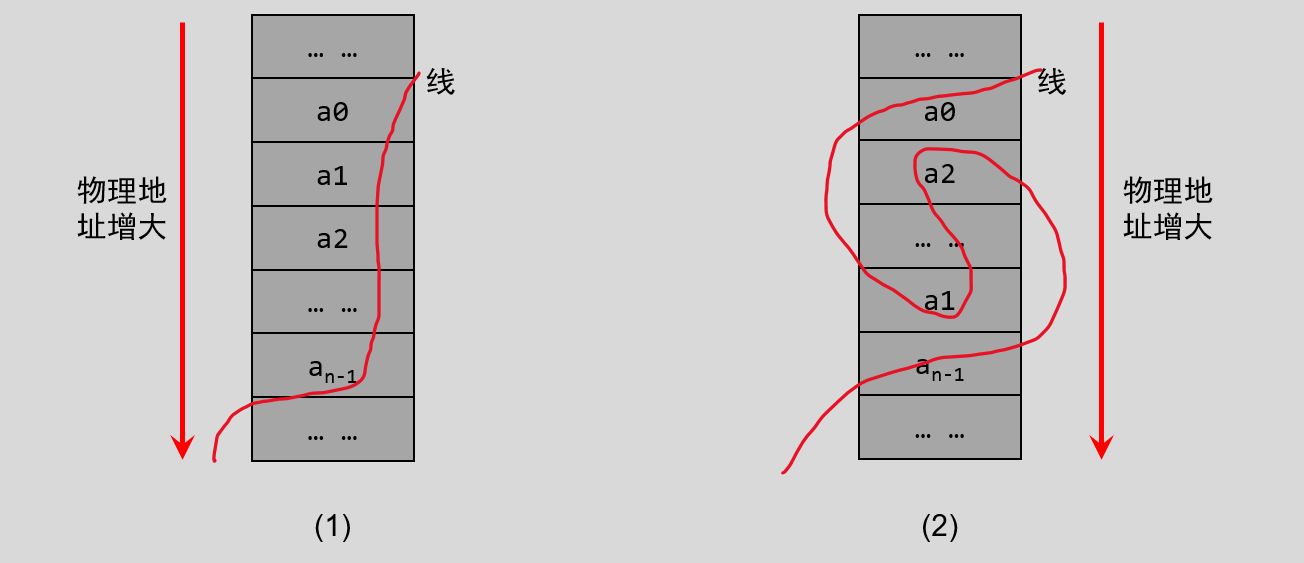
图中的(1),将数据依次存储在连续的整块物理空间中,这种存储结构称为顺序存储结构(简称顺序表);图中的(2),将数据分散的存储在物理空间中,通过一根线保存着它们之间的逻辑关系,这种存储结构称为链式存储结构(简称链表)。所以说线性表可以分为顺序表和链表两种,后续会进行详细的学习。
三、前驱与后继
某一元素的左侧相邻元素称为直接前驱,位于此元素左侧的所有元素都统称为前驱元素;某一元素的右侧相邻元素称为直接后继,位于此元素右侧的所有元素都统称为后继元素。例如
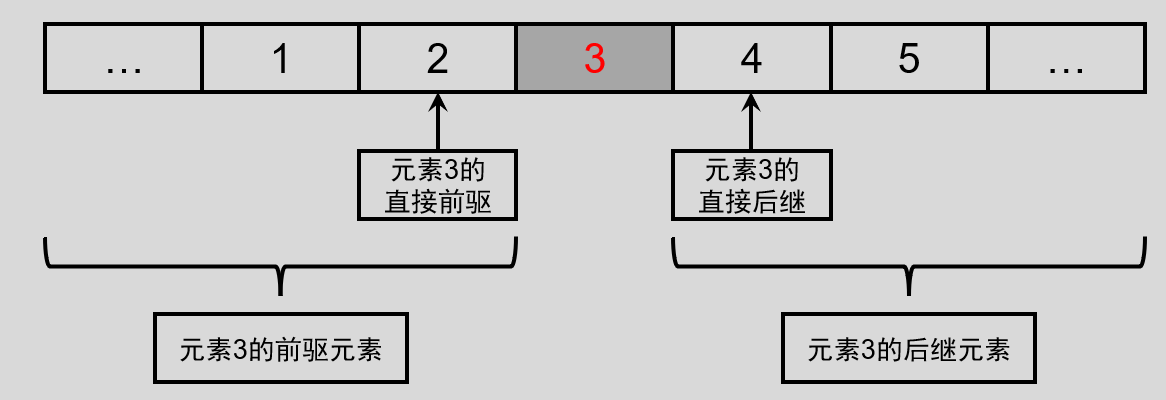
- 线性表的前驱和后继特征
对非空线性表 L 来说:
(1)$a_0$是表头,无前驱;
(2) $a_{n-1}$是表尾,无后继。
(3)其它的每个元素 $a_i$ 有且仅有一个直接前驱 $a_{ i -1}$ 和一个直接后继 $a_{i+1}$ 。